Chapter 3 - Linear regression: the basics¶
import warnings
import pandas as pd
import proplot as plot
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from scipy import stats
warnings.filterwarnings("ignore")
%pylab inline
plt.rcParams["axes.labelweight"] = "bold"
plt.rcParams["font.weight"] = "bold"
Populating the interactive namespace from numpy and matplotlib
kidiq_df = pd.read_csv("../data/kidiq.tsv.gz", sep="\t")
kidiq_df.head()
| kid_score | mom_hs | mom_iq | mom_work | mom_age | |
|---|---|---|---|---|---|
| 0 | 65 | 1.0 | 121.117529 | 4 | 27 |
| 1 | 98 | 1.0 | 89.361882 | 4 | 25 |
| 2 | 85 | 1.0 | 115.443165 | 4 | 27 |
| 3 | 83 | 1.0 | 99.449639 | 3 | 25 |
| 4 | 115 | 1.0 | 92.745710 | 4 | 27 |
The data represents cognitive test-scores of three- and four-year-old children given characteristics of their mothers, using data from a survey of adult American women and their children.
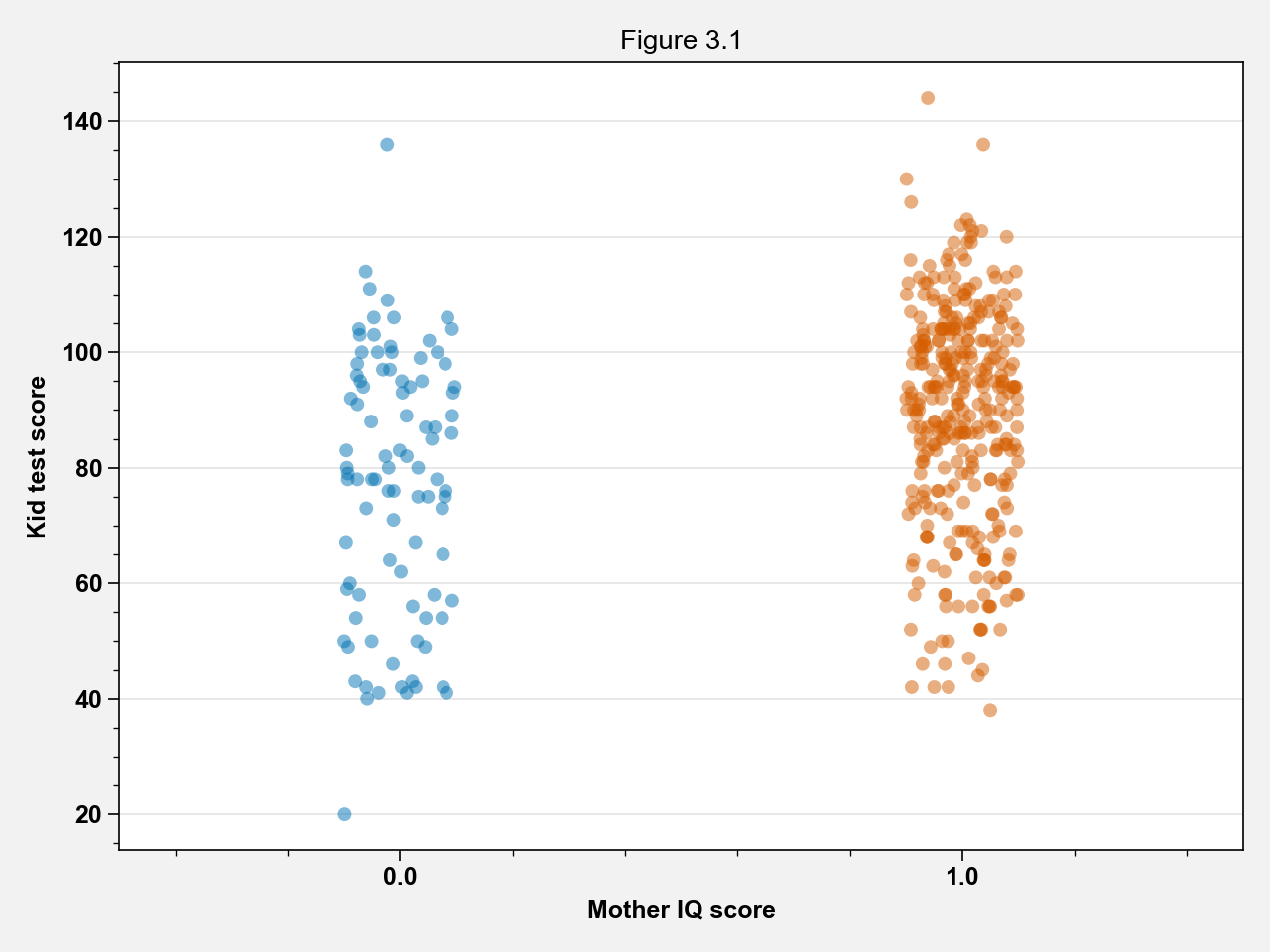
Figure 3.1¶
fig, ax = plt.subplots()
sns.stripplot(x="mom_hs", y="kid_score", data=kidiq_df, ax=ax, alpha=0.5)
ax.set_xlabel("Mother IQ score")
ax.set_ylabel("Kid test score")
ax.set_title("Figure 3.1")
fig.tight_layout()
One predictor¶
Binary predictor¶
model = sm.OLS(kidiq_df["kid_score"], sm.add_constant(kidiq_df[["mom_hs"]]))
model = smf.ols(formula="""kid_score ~ mom_hs""", data=kidiq_df)
results_hs = model.fit()
print(results_hs.summary())
OLS Regression Results
==============================================================================
Dep. Variable: kid_score R-squared: 0.056
Model: OLS Adj. R-squared: 0.054
Method: Least Squares F-statistic: 25.69
Date: Sat, 20 Jun 2020 Prob (F-statistic): 5.96e-07
Time: 22:37:21 Log-Likelihood: -1911.8
No. Observations: 434 AIC: 3828.
Df Residuals: 432 BIC: 3836.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 77.5484 2.059 37.670 0.000 73.502 81.595
mom_hs 11.7713 2.322 5.069 0.000 7.207 16.336
==============================================================================
Omnibus: 11.077 Durbin-Watson: 1.464
Prob(Omnibus): 0.004 Jarque-Bera (JB): 11.316
Skew: -0.373 Prob(JB): 0.00349
Kurtosis: 2.738 Cond. No. 4.11
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Thus,
\[\mathrm{kid\_score} = 78 + 12 . \mathrm{mom\_hs} + \mathrm{error}\]
This model summarized the difference in average test scores between children of mothers who completed high school against those who did not.
\[\begin{split}\begin{align*}
78 &= \text{Average predicted score for children}\\
& \text{whose mothers did not complete high school}\\
78 + 12 &= \text{Average predicted score for children}\\
&\text{whose mothers did complete high school}
\end{align*}\end{split}\]
Thus, children whose mothers have completed high school score 12 points higher on average than children of methoers who haven’t.
Continuous predictor¶
model = smf.ols(formula="""kid_score ~ mom_iq + 1""", data=kidiq_df)
results_iq = model.fit()
print(results_iq.summary())
OLS Regression Results
==============================================================================
Dep. Variable: kid_score R-squared: 0.201
Model: OLS Adj. R-squared: 0.199
Method: Least Squares F-statistic: 108.6
Date: Sat, 20 Jun 2020 Prob (F-statistic): 7.66e-23
Time: 22:37:21 Log-Likelihood: -1875.6
No. Observations: 434 AIC: 3755.
Df Residuals: 432 BIC: 3763.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 25.7998 5.917 4.360 0.000 14.169 37.430
mom_iq 0.6100 0.059 10.423 0.000 0.495 0.725
==============================================================================
Omnibus: 7.545 Durbin-Watson: 1.645
Prob(Omnibus): 0.023 Jarque-Bera (JB): 7.735
Skew: -0.324 Prob(JB): 0.0209
Kurtosis: 2.919 Cond. No. 682.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
\[\mathrm{kid\_score} = 26 + 0.6 . \mathrm{mom\_hs} + \mathrm{error}\]
results_iq_hs = smf.ols(
formula="""kid_score ~ mom_iq + mom_hs + 1""", data=kidiq_df
).fit()
print(results_iq_hs.summary())
OLS Regression Results
==============================================================================
Dep. Variable: kid_score R-squared: 0.214
Model: OLS Adj. R-squared: 0.210
Method: Least Squares F-statistic: 58.72
Date: Sat, 20 Jun 2020 Prob (F-statistic): 2.79e-23
Time: 22:37:21 Log-Likelihood: -1872.0
No. Observations: 434 AIC: 3750.
Df Residuals: 431 BIC: 3762.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 25.7315 5.875 4.380 0.000 14.184 37.279
mom_iq 0.5639 0.061 9.309 0.000 0.445 0.683
mom_hs 5.9501 2.212 2.690 0.007 1.603 10.297
==============================================================================
Omnibus: 7.327 Durbin-Watson: 1.625
Prob(Omnibus): 0.026 Jarque-Bera (JB): 7.530
Skew: -0.313 Prob(JB): 0.0232
Kurtosis: 2.845 Cond. No. 683.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
\[\mathrm{kid\_score} = 26 + 6.\mathrm{mom\_hs} + 0.6.\mathrm{mom\_iq}\]
Interpretation:
Intercept (26): If a child had a mother who did not complete high school and an IQ of 0, then we would predict this child’s test score to be 26.
Coeff of mom_hs (6): If the mothers had same IQ, then a child whose mother went to high school will have 6 additional points as compared to the child whose mother did not go to high school.
Coeff of mom_iq (0.6): Comparing children with same value of mom_hs, if mother IQ differs by 1 then children are expected to have a difference of 0.6 points.
Interaction¶
results_iq_hs_interaction = smf.ols(
formula="""kid_score ~ mom_hs + mom_iq + mom_hs:mom_iq""", data=kidiq_df
).fit()
print(results_iq_hs_interaction.summary())
OLS Regression Results
==============================================================================
Dep. Variable: kid_score R-squared: 0.230
Model: OLS Adj. R-squared: 0.225
Method: Least Squares F-statistic: 42.84
Date: Sat, 20 Jun 2020 Prob (F-statistic): 3.07e-24
Time: 22:37:21 Log-Likelihood: -1867.5
No. Observations: 434 AIC: 3743.
Df Residuals: 430 BIC: 3759.
Df Model: 3
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
Intercept -11.4820 13.758 -0.835 0.404 -38.523 15.559
mom_hs 51.2682 15.338 3.343 0.001 21.122 81.414
mom_iq 0.9689 0.148 6.531 0.000 0.677 1.260
mom_hs:mom_iq -0.4843 0.162 -2.985 0.003 -0.803 -0.165
==============================================================================
Omnibus: 8.014 Durbin-Watson: 1.660
Prob(Omnibus): 0.018 Jarque-Bera (JB): 8.258
Skew: -0.333 Prob(JB): 0.0161
Kurtosis: 2.887 Cond. No. 3.10e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.1e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Interpretation¶
\[\mathrm{kid\_score} = -11 + 51.2.\mathrm{mom\_hs} + 1.1.\mathrm{mom\_iq} - 0.5 \mathrm{mom\_hs:mom\_iq}\]
Intercept (-12_: Predicted score for children whose mothers did not finish high school and have an IQ of 0. This is impossible scenario.
Coeff of mom_hs: Difference of predicted kids’s score with mothers whose high school status is the same = mothers did not complete high school and had an IQ of 0 and those whose mothers did complete high school but had an IQ of 0
Coeff of mom_iq: Difference of predicted kids’ score with mothers who did not complete high school but whose mothers had an IQ difference of 1.
Coeff of mom_hs:mom_iq: Difference in slope for mom_iq comparing children with mothers who did and did not complete
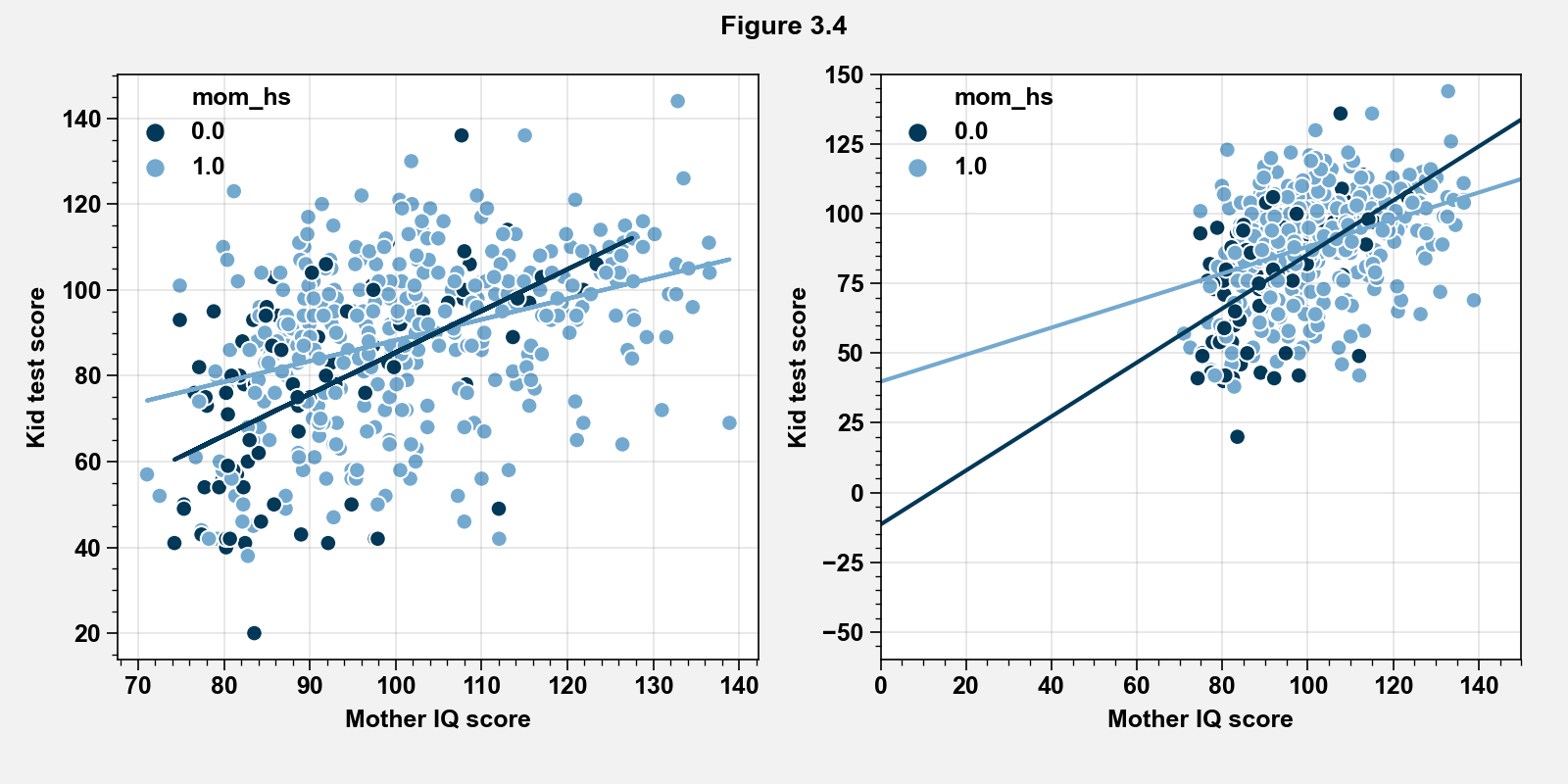
It is also possible to see the interpretation of the interaction term by breaking it down into two categories: children with mom_hs = 1 and children with mom_hs = 0:
mom_hs = 0: \begin{align*}\mathrm{kid_score} &= -11 + 51.2(0) + 1.1.\mathrm{mom_iq}\ &= -11 + 1.1.\mathrm{mom_iq} \end{align*}
mom_hs = 1: \begin{align*}\mathrm{kid_score} &= -11 + 51.2(1) + 1.1.\mathrm{mom_iq} - 0.5.1.\mathrm{mom_iq}\ &= 40 + 0.6.\mathrm{mom_iq} \end{align*}
kidiq_hs1 = kidiq_df.loc[kidiq_df.mom_hs == 1]
kidiq_hs0 = kidiq_df.loc[kidiq_df.mom_hs == 0]
results_iq_hs_interaction = smf.ols(
formula="""kid_score ~ mom_hs + mom_iq + mom_hs:mom_iq""", data=kidiq_df
).fit()
line_hs1 = (
results_iq_hs_interaction.params[0]
+ results_iq_hs_interaction.params[1] * kidiq_hs1["mom_hs"]
+ results_iq_hs_interaction.params[2] * kidiq_hs1["mom_iq"]
+ results_iq_hs_interaction.params[3] * kidiq_hs1["mom_hs"] * kidiq_hs1["mom_iq"]
)
line_hs0 = (
results_iq_hs_interaction.params[0]
+ results_iq_hs_interaction.params[1] * kidiq_hs0["mom_hs"]
+ results_iq_hs_interaction.params[2] * kidiq_hs0["mom_iq"]
+ results_iq_hs_interaction.params[3] * kidiq_hs0["mom_hs"] * kidiq_hs0["mom_iq"]
)
fig = plt.figure(figsize=(8, 4))
ax = plt.subplot(121)
palette = {0: "#023858", 1: "#74a9cf"}
sns.scatterplot(x="mom_iq", y="kid_score", hue="mom_hs", data=kidiq_df, palette=palette)
ax.plot(kidiq_hs1["mom_iq"], line_hs1, color=palette[1])
ax.plot(kidiq_hs0["mom_iq"], line_hs0, color=palette[0])
ax.set_xlabel("Mother IQ score")
ax.set_ylabel("Kid test score")
ax.legend(frameon=False)
ax = plt.subplot(122)
palette = {0: "#023858", 1: "#74a9cf"}
sns.scatterplot(x="mom_iq", y="kid_score", hue="mom_hs", data=kidiq_df, palette=palette)
ax.set_xlim(0, 150)
ax.set_ylim(-60, 150)
m, b = np.polyfit(kidiq_hs1["mom_iq"], line_hs1, 1)
xpoints = np.linspace(0, 150, 1000)
ax.plot(xpoints, xpoints * m + b, color=palette[1])
m, b = np.polyfit(kidiq_hs0["mom_iq"], line_hs0, 1)
ax.plot(xpoints, xpoints * m + b, color=palette[0])
ax.set_xlabel("Mother IQ score")
ax.set_ylabel("Kid test score")
ax.legend(frameon=False)
fig.suptitle("Figure 3.4")
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
Fitting and summarizing regressions¶
results_hs_iq = smf.ols(formula="""kid_score ~ mom_hs + mom_iq""", data=kidiq_df).fit()
print(results_hs_iq.summary())
OLS Regression Results
==============================================================================
Dep. Variable: kid_score R-squared: 0.214
Model: OLS Adj. R-squared: 0.210
Method: Least Squares F-statistic: 58.72
Date: Sat, 20 Jun 2020 Prob (F-statistic): 2.79e-23
Time: 22:37:21 Log-Likelihood: -1872.0
No. Observations: 434 AIC: 3750.
Df Residuals: 431 BIC: 3762.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 25.7315 5.875 4.380 0.000 14.184 37.279
mom_hs 5.9501 2.212 2.690 0.007 1.603 10.297
mom_iq 0.5639 0.061 9.309 0.000 0.445 0.683
==============================================================================
Omnibus: 7.327 Durbin-Watson: 1.625
Prob(Omnibus): 0.026 Jarque-Bera (JB): 7.530
Skew: -0.313 Prob(JB): 0.0232
Kurtosis: 2.845 Cond. No. 683.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
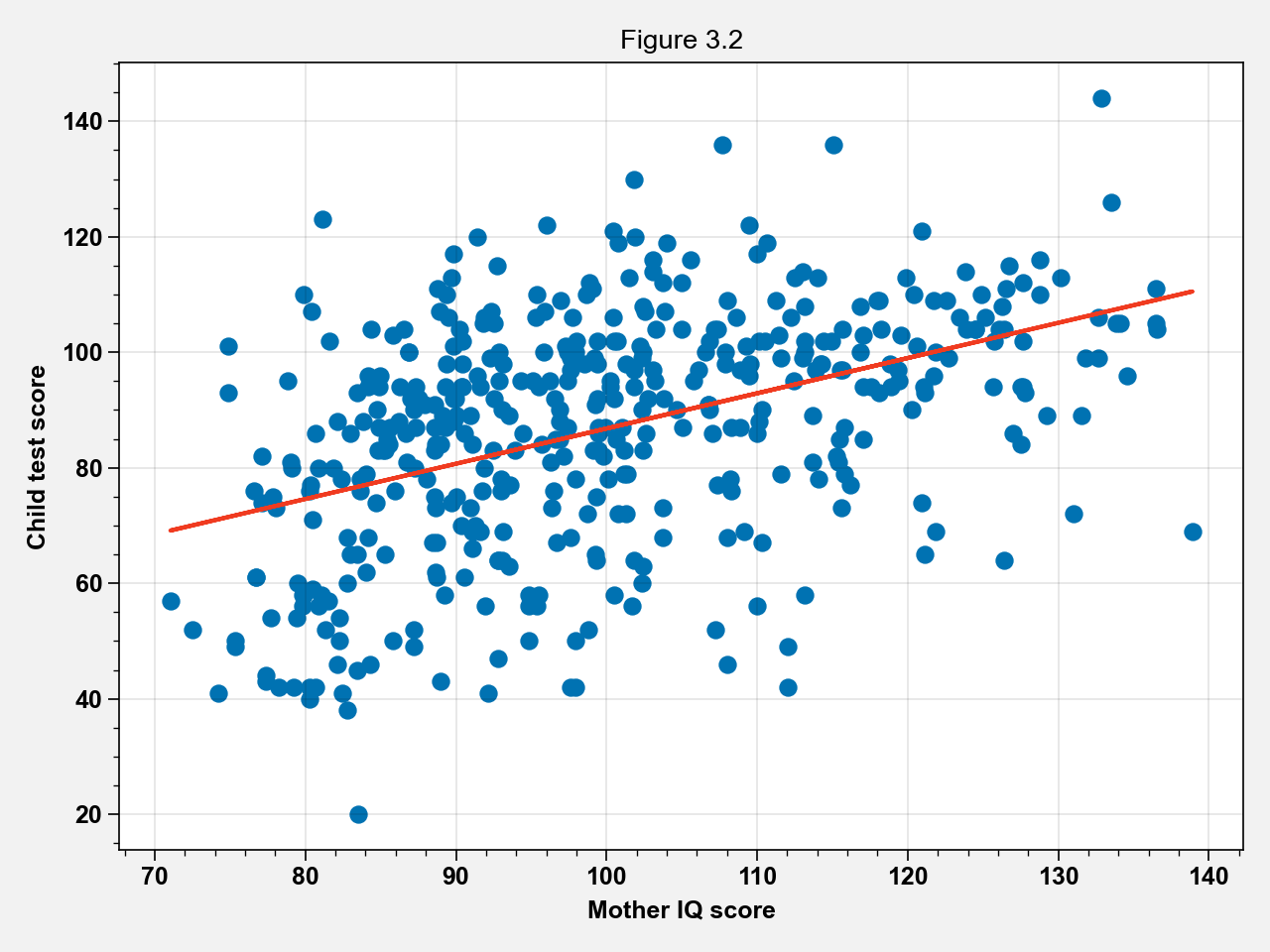
Displaying a regression line as a function of one input variable¶
results_iq = smf.ols(formula="""kid_score ~ mom_iq""", data=kidiq_df).fit()
print(results_iq.summary())
OLS Regression Results
==============================================================================
Dep. Variable: kid_score R-squared: 0.201
Model: OLS Adj. R-squared: 0.199
Method: Least Squares F-statistic: 108.6
Date: Sat, 20 Jun 2020 Prob (F-statistic): 7.66e-23
Time: 22:37:22 Log-Likelihood: -1875.6
No. Observations: 434 AIC: 3755.
Df Residuals: 432 BIC: 3763.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 25.7998 5.917 4.360 0.000 14.169 37.430
mom_iq 0.6100 0.059 10.423 0.000 0.495 0.725
==============================================================================
Omnibus: 7.545 Durbin-Watson: 1.645
Prob(Omnibus): 0.023 Jarque-Bera (JB): 7.735
Skew: -0.324 Prob(JB): 0.0209
Kurtosis: 2.919 Cond. No. 682.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
fig, ax = plt.subplots()
ax.scatter(kidiq_df["mom_iq"], kidiq_df["kid_score"])
line = results_iq.params[0] + results_iq.params[1] * kidiq_df["mom_iq"]
ax.plot(kidiq_df["mom_iq"], line, color="#f03b20")
ax.set_title("Figure 3.2")
ax.set_xlabel("Mother IQ score")
ax.set_ylabel("Child test score")
fig.tight_layout()
kidiq_hs1 = kidiq_df.loc[kidiq_df.mom_hs == 1]
kidiq_hs0 = kidiq_df.loc[kidiq_df.mom_hs == 0]
results_iq_hs1 = smf.ols(formula="""kid_score ~ mom_iq + 1""", data=kidiq_hs1).fit()
results_iq_hs0 = smf.ols(formula="""kid_score ~ mom_iq + 1""", data=kidiq_hs0).fit()
results_iq_hs = smf.ols(
formula="""kid_score ~ mom_iq + mom_hs + 1""", data=kidiq_df
).fit()
line_hs1 = results_iq_hs1.params[0] + results_iq_hs1.params[1] * kidiq_hs1["mom_iq"]
line_hs0 = results_iq_hs0.params[0] + results_iq_hs0.params[1] * kidiq_hs0["mom_iq"]
line_hs1 = (
results_iq_hs.params[0]
+ results_iq_hs.params[1] * kidiq_hs1["mom_iq"]
+ results_iq_hs.params[2] * kidiq_hs1["mom_hs"]
)
line_hs0 = (
results_iq_hs.params[0]
+ results_iq_hs.params[1] * kidiq_hs0["mom_iq"]
+ results_iq_hs.params[2] * kidiq_hs0["mom_hs"]
)
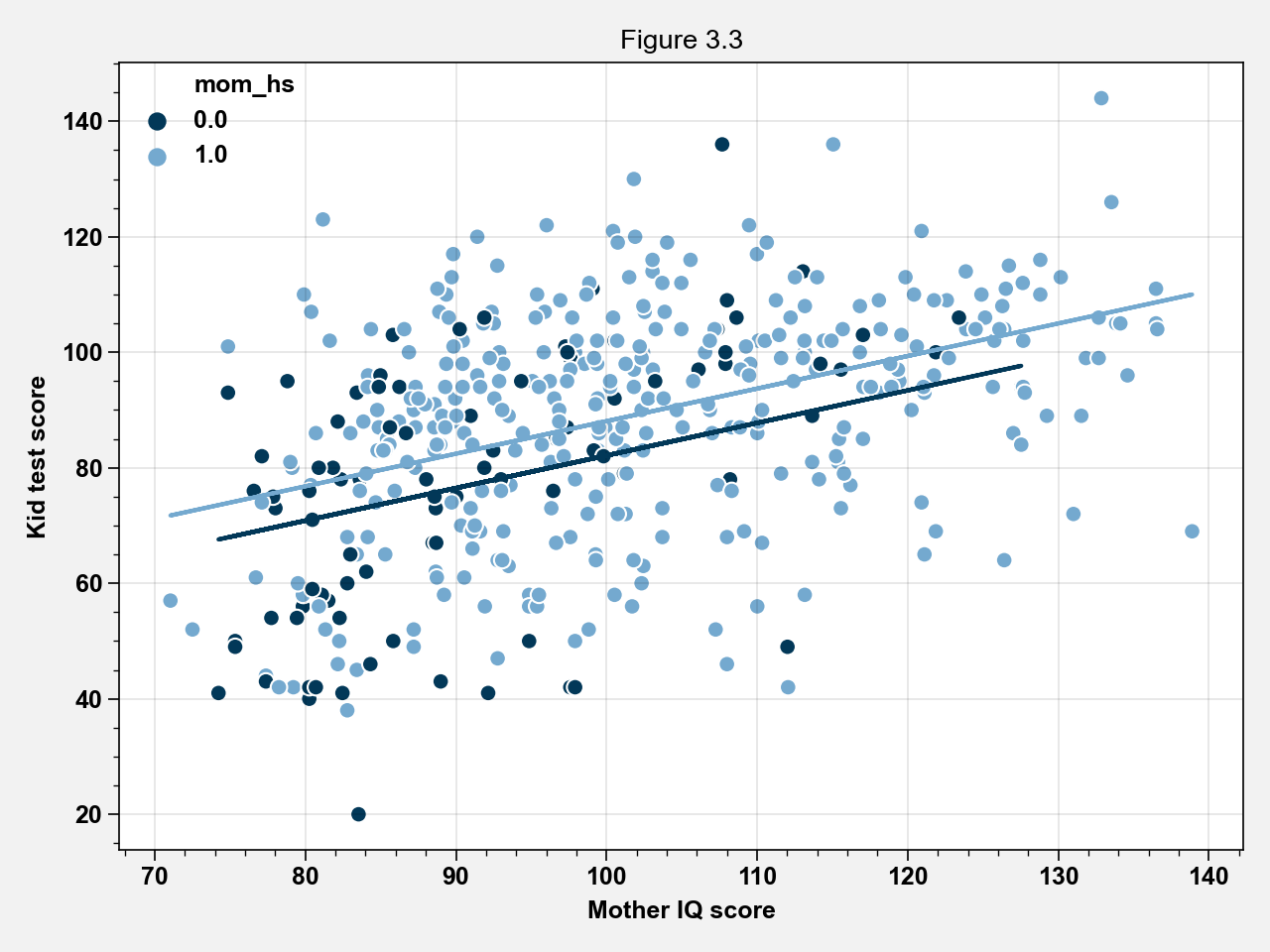
fig, ax = plt.subplots()
palette = {0: "#023858", 1: "#74a9cf"}
sns.scatterplot(x="mom_iq", y="kid_score", hue="mom_hs", data=kidiq_df, palette=palette)
ax.plot(kidiq_hs1["mom_iq"], line_hs1, color=palette[1])
ax.plot(kidiq_hs0["mom_iq"], line_hs0, color=palette[0])
ax.set_xlabel("Mother IQ score")
ax.set_ylabel("Kid test score")
ax.legend(frameon=False)
ax.set_title("Figure 3.3")
fig.tight_layout()
TODO: Displaying uncertainity in the fitted regression¶
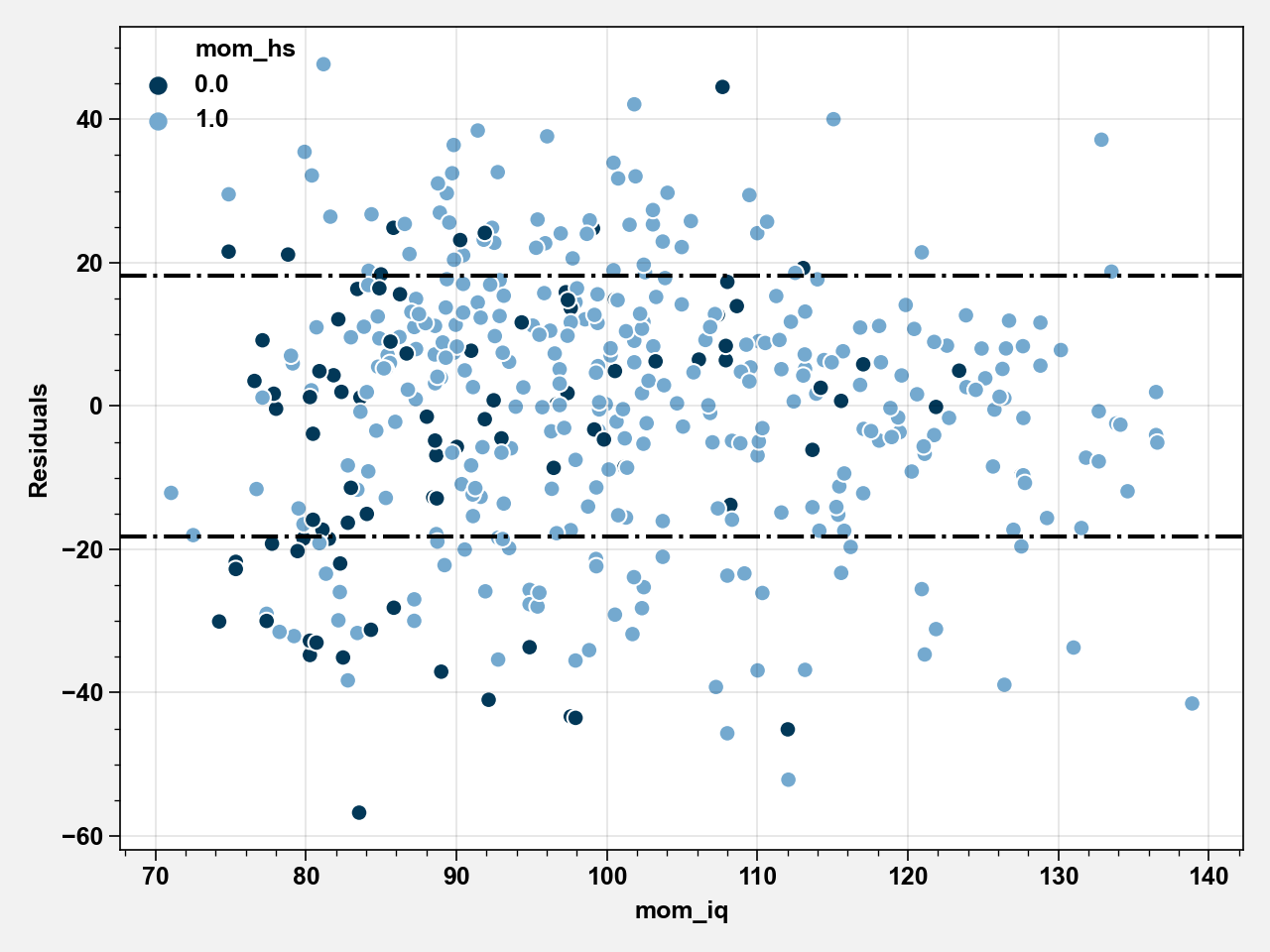
Plotting residuals¶
results_iq = smf.ols(formula="""kid_score ~ mom_iq""", data=kidiq_df).fit()
kidiq_df["Residuals"] = results_iq.resid
sd = kidiq_df["Residuals"].std()
fig, ax = plt.subplots()
palette = {0: "#023858", 1: "#74a9cf"}
sns.scatterplot(x="mom_iq", y="Residuals", hue="mom_hs", data=kidiq_df, palette=palette)
ax.axhline(y=sd * 1, linestyle="-.", color="black")
ax.axhline(y=sd * -1, linestyle="-.", color="black")
ax.legend(frameon=False)
fig.tight_layout()
