Problem 1¶
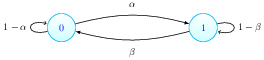
The transition matrix is given by: $$ \begin{bmatrix} 1-\alpha & \alpha\\ \beta & 1-\beta \end{bmatrix} $$
Part (a)¶
$\eta = min(n>0, X_n=1)$ given $X_0=0$
To Prove $\eta \sim Geom(\alpha)$
$\eta = P(X_0=0,X_1=0, \dots X_{n-1}=1, X_n=1)$
Using the Markov property this can be written as:
$$ \eta = P(X_0=0)P(X_1=0|X_0=0)P(X_2=0|X_1=0)P(X_3=0|X_2=0) \dots P(X_{n-1}=0|X_{n-2}=0)P(X_{n}=1|X_{n-1}=0) $$And being time-homogenous, this simplifies to:
$$ \eta = P(X_0=0)\big(P(X_1=0|X_0)\big)^{n-1}\times P(X_1=1|X_0=0) $$$\implies$
$$ \eta = P(X_0=0)\big(1-\alpha)^{n-1}\alpha = \big(1-\alpha)^{n-1}\alpha $$And hence $\eta \sim Geom(\alpha)$
Part (b)¶
Spectral decomposition of $P$ and value for $P(X_n=1|X_0=0)$
Spectral decomposition of $P$:
$$ det\begin{bmatrix} \alpha-\lambda & 1-\alpha\\ 1-\beta & \beta-\lambda \end{bmatrix} = 0 $$$$ \lambda^2 +(\alpha + \beta-2) \lambda + (1-\alpha -\beta) = 0 $$Thus, $\lambda_1 = 1$ and $\lambda_2 = 1-\alpha-\beta$
Eigenvectors are given by:
$v_1^T = \big( x_1\ x_1 \big)\ \forall\ x_1 \in R$
and for $\lambda_2$ , $v_2 = \big( x_1\ \frac{-\beta x_1}{\alpha} \big)$
Now using Markov property: $P(X_n=1|X_0=0) = (P^n)_{01}$
Now,
$P^n = VD^nV^{-1}$
where: $$ V = \begin{bmatrix} 1 & 1\\ 1 & \frac{-\beta}{\alpha} \end{bmatrix} $$
and
$$ D = \begin{bmatrix} 1 & 0 \\ 0 & (1-\alpha-\beta) \end{bmatrix} $$$$ V^{-1} = \frac{-1}{\frac{\beta}{\alpha}+1}\begin{bmatrix} -\frac{\beta}{\alpha} & -1 \\ -1 & 1 \end{bmatrix} $$Thus,
$$ P^n = \begin{bmatrix} 1 & 1\\ 1 & \frac{-\beta}{\alpha} \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & (1-\alpha-\beta)^n \end{bmatrix} \times \frac{-1}{\frac{\beta}{\alpha}+1}\begin{bmatrix} -\frac{\beta}{\alpha} & -1 \\ -1 & 1 \end{bmatrix} $$$$ P^n = \frac{1}{\alpha+\beta} \begin{bmatrix} \beta + \alpha(1-\alpha-\beta)^n & \alpha-\alpha(1-\alpha-\beta)^n\\ \beta - \beta(1-\alpha-\beta)^n & \alpha + \beta(1-\alpha-\beta)^n \end{bmatrix} $$Part (c)¶
When $\alpha+\beta=1$, the eigen values are $\lambda_1=1$ and $\lambda_2=0$ and hence
$$ P^n = \begin{bmatrix} \beta & \alpha \\ \beta & \alpha \end{bmatrix} $$Check:
Also consider the following identifiy: $P^{n+1}=PP^n$
then:
$$ \begin{bmatrix} p_{00}^{n+1} & p_{01}^{n+1}\\ p_{10}^{n+1} & p_{11}^{n+1}\\ \end{bmatrix} = \begin{bmatrix} p_{00}^n & p_{01}^n\\ p_{10}^n & p_{11}^n \end{bmatrix} \times \begin{bmatrix} 1-\alpha & \alpha\\ \beta & 1-\beta \end{bmatrix} $$$\implies$
$$ \begin{align} p_{11}^{n+1} &= p_{10}^n(\alpha) + p_{11}^n(1-\beta)\\ &= (1-p_{11}^n)(\alpha) +(p_{11}^n)(1-\beta)\\ &= \alpha + (1-\alpha-\beta)p_{11}^n \end{align} $$Consider the recurrence:
$$ x_{n+1} = \alpha+(1-\alpha-\beta)x_n $$Constant solution $x_n=x_{n+1}=x$ is given by: $x=\frac{\alpha}{\alpha+\beta}$
Now let $y_n = x_n-x=x_n-\frac{\alpha}{\alpha+\beta}$ then,
$y_{n+1} = (1-\alpha-\beta)y_n$ and hence $y_n=(1-\alpha-\beta)^n y_0$
Thus, $$p_{11}^{n} = (1-\alpha-\beta)^np_{11}^0 +\frac{\alpha}{\alpha+\beta}$$
Given $P_{00}=\frac{\beta}{\alpha+\beta}$ and $\alpha+\beta=1$ and hence:
$p_{11}^n = \frac{\alpha}{\alpha+\beta} = \alpha$
and hence, $p_{10}^n = \beta$
Similary,
$p_{00}^n = \beta$ and $p_{01}^n = \alpha$
Problem 2¶
$P(X_1=0) \frac{\beta}{\alpha+\beta}$ and hence $P(X_1=1) = \frac{\alpha}{\alpha+\beta}$
$X=X_1X_2\dots X_n$ and $Y=Y_1Y_2\dots Y_n$ representes the reverse string $Y_k=X_{n+k-1}$
Part (a)¶
Given string of digits: $a_1,a_2,a_3 \dots a_n $ to find: $P(Y_1=a_1,Y_2=a_2,Y_3=a_3\dots Y_n=a_n)$
$$ \begin{align} P(Y_1=a_1,Y_2=a_2,Y_3=a_3\dots Y_n=a_n) &= P(X_1=a_n,X_2=a_{n-1}, \dots X_n=a_1) \\ &= P(X_1=a_n)P(X_2=a_{n-1}|X_1=a_n)P(X_3=a_{n-2}|X_2=a_{n-1})\dots P(X_n=a_1|X_{n-1}=a_2) \\ &= P(X_1=a_n)(P_{a_n a_{n-1}})(P_{a_{n-1} a_{n-2}}) \dots (P_{a_2 a_1}) \end{align} $$The problem asked about not using spectral decomposition, but I was not sure how spectral decomposition would have come in handy if the states $a_i$ are not specified explicitly.
Part (b)¶
$$ z=\begin{cases} X & if \theta = H\\ Y & otherwise \end{cases} $$Given function f such that, $f :\{0,1\}^n \longrightarrow \{H,T\}$ To show: $P(f(Z)=\theta)=0.5$
$P(\theta=H) = P(\theta=T) = 0.5$
Given Z, guess $\theta$:
$P(\theta=H|Z=X) = \frac{P(\theta=H, Z=X)}{P(Z=X)}$
Z, has only two possible values: $H$ and $T$ and hence assuming the guess function is unbiased:
$P(f(Z)=H) = P(f(Z)=T)=0.5$
Problem 3¶
$$ \tau = min\{ n \geq 0: X_n=\dagger\} $$$$ E[\tau] = E_a[E_a[\tau|X_n=a]\ where\ a \in \{\phi, \alpha, \beta, \alpha+\beta, pol, \dagger\} $$Let $S=\{\phi, \alpha, \beta, \alpha+\beta, pol, \dagger\}$
Consider for $a\neq \dagger$: $$ h(a) = E[\tau|X_0=a] = \sum_{s \in S}P_{as} \times (1) + P_{as}\times E[\tau|X_0=s) $$
$\implies$
$$ h(a) = ((I-P_{-})^{-1})_a $$where $P_{-}$ represents the matrix with the row and column representng $X_i=\dagger$ removed.
%matplotlib inline
from __future__ import division
import numpy as np
from numpy import linalg as LA
k_a=0.2
k_b=0.2
k_p = 0.5
P = np.matrix([[1-k_a-k_b, k_a ,k_b, 0, 0, 0],
[k_a, 1-k_a-k_b, 0, k_b, 0, 0],
[k_b, 0, 1-k_a-k_b, k_a, 0, 0],
[0, k_b, k_a, 1-k_a-k_b-k_p, k_p, 0],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 1, 0, 0]])
q = [[k_a-k_b,k_a,k_b,0,0],
[k_a,k_a+k_b,0,k_b,0],
[k_b,0,k_a+k_b,0,0],
[0,k_b,k_a,k_a+k_b+k_p,k_p],
[0,0,0,0,0]]
qq = np.array(q)
print(P)
states = ['phi', 'alpha', 'beta', 'ab', 'pol', 'd']
import networkx as nx
G=nx.from_numpy_matrix(P,create_using=nx.MultiDiGraph())
G.edges(data=True)
#nx.draw_graphviz(G)# labels=states)
nx.write_dot(G,'G.dot')
!neato -T png G.dot > multi.png
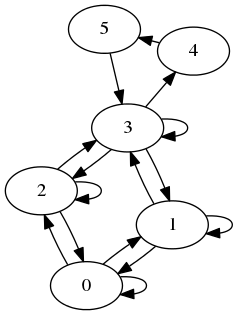
The markov chain seems to be irreducible One way to obtain the stationary state is to look at the eigen vectors correspendoing to the eigen value of 1. However, the eigen vectors come out to be imaginary. This seemed to be an issue wwith the solver so I relied on solving the system of equation: $\pi = P\pi$
w, v = LA.eig(P)
for i in range(0,6):
print 'Eigen value: {}\n Eigen vector: {}\n'.format(w[i],v[:,i])
## Solve for (I-Q)^{-1}
iq = np.linalg.inv(np.eye(5)-qq)
iq_phi = iq[0,0]
iq_alpha = iq[1,1]
iq_beta = iq[2,2]
iq_alphabeta = iq[3,3]
iq_pol = iq[4,4]
EDIT: I made correction to solve for corrected $\pi$, by acounting for $P^T$ and not $P$
A = np.eye(6)-P.T
A[-1,:] = [1,1,1,1,1,1]
B = [0,0,0,0,0,1]
X=np.linalg.solve(A,B)
print(X)
Stationary state is given by $\pi = (0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.1667)$ The mean number of visits per unit time to $\dagger$ are $\frac{1}{\pi_6} = 6$ However strangely this does not satisfy $\pi=P\pi$. I was not able to figure out where I went wrong.
EDIT: I made correction to solve for corrected $\pi$, by acounting for $P^T$ and not $P$, so this no longer holds
#EDIT: I made correction to solve for corrected $\pi$, by acounting for $P^T$ and not $P$
print('\pi*P={}\n'.format(X*P))
print('But \pi={}'.format(X))
Simulating the chain:
General strategy: Generate a random number $\longrightarrow$ Select a state $\longrightarrow$ Jump to state $\longrightarrow$ Repeat
## phi
np.random.seed(1)
PP = {}
PP['phi']= [1-k_a-k_b, k_a ,k_b, 0, 0, 0]
PP['alpha'] = [k_a, 1-k_a-k_b, 0, k_b, 0, 0]
PP['beta'] = [k_b, 0, 1-k_a-k_b, k_a, 0, 0]
PP['ab']= [0, k_b, k_a, 1-k_a-k_b-k_p, k_p, 0]
PP['pol']= [0, 0, 0, 0, 0, 1]
PP['d']= [0, 0, 0, 1, 0, 0]
##For $h(\phi)$
x0='phi'
x='phi'
def h(x):
s=0
new_state=x
for i in range(1,1000):
old_state=new_state
probs = PP[old_state]
z=np.random.choice(6, 1, p=probs)
new_state = states[z[0]]
#print('{} --> {}'.format(old_state, new_state))
s+=z[0]
return s/1000
Part (a,b,c)¶
print(r'$h(\phi)$: From simulation: {}; From calculation: {}'.format(h('phi'),iq_phi))
print(r'$h(\alpha)$: From simulation: {}; From calculation: {}'.format(h('alpha'),iq_alpha))
print(r'$h(\beta)$: From simulation: {}; From calculation: {}'.format(h('beta'),iq_beta))
print(r'$h(\alpha+\beta)$: From simulation: {}; From calculation: {}'.format(h('ab'),iq_alphabeta))
print(r'$h(\pol)$: From simulation: {}; From calculation: {}'.format(h('pol'),iq_pol))
old_state = [0.1,0.2,0.3,0.4,0,0]
def perturb(old_state):
new_state = old_state*P
return new_state
new_state = [0,0,0,0,0,1]
while not np.allclose(old_state, new_state):
old_state, new_state = new_state, perturb(old_state)
print old_state
# EDIT: I made correction to solve for corrected $\pi$, by acounting for $P^T$ and not $P$
print('From calculation(which is NO LONGER wrong!), stationary distribution:{}'.format(X))
print('From simulation, stationary distribution: {}'.format(old_state))