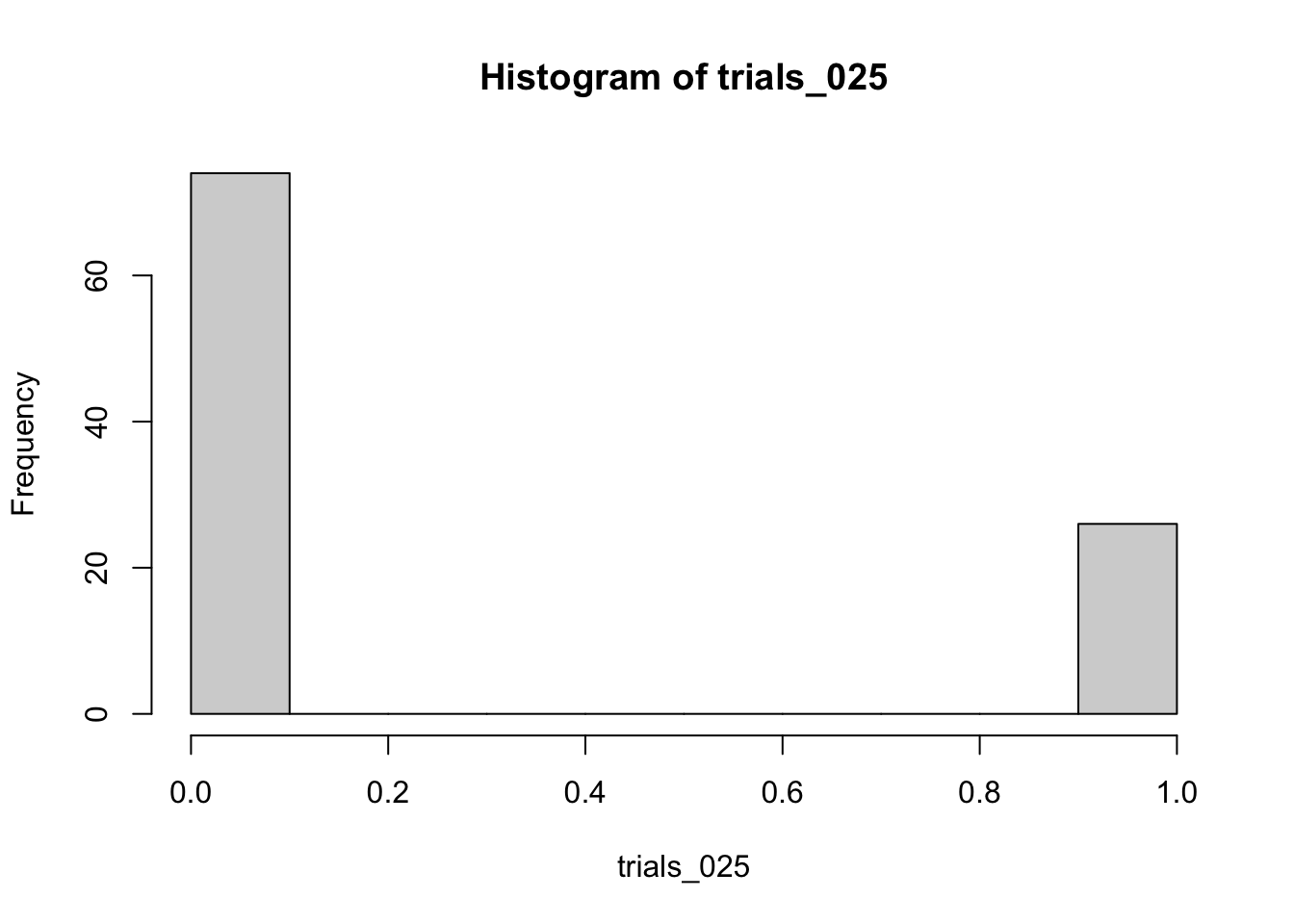
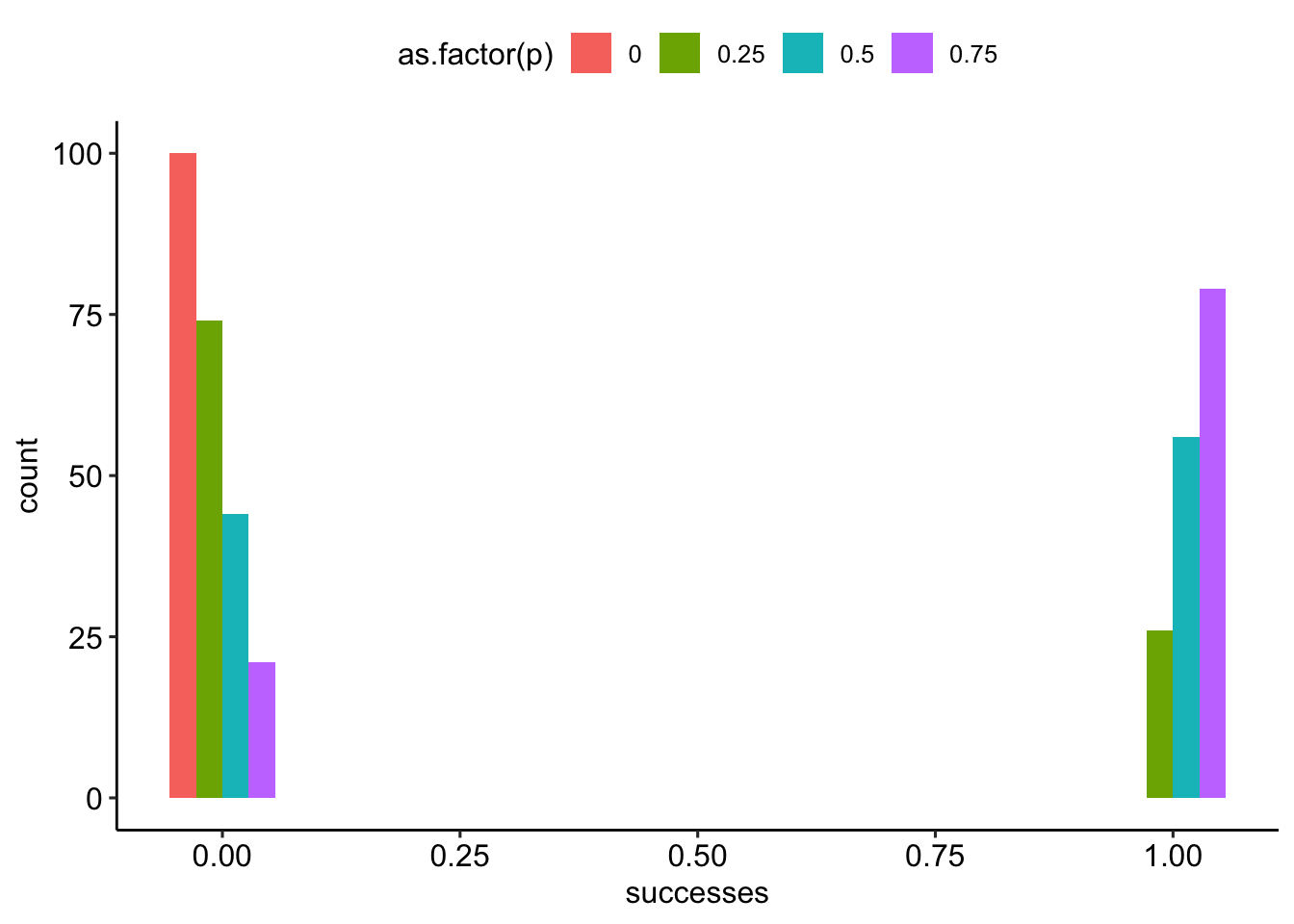
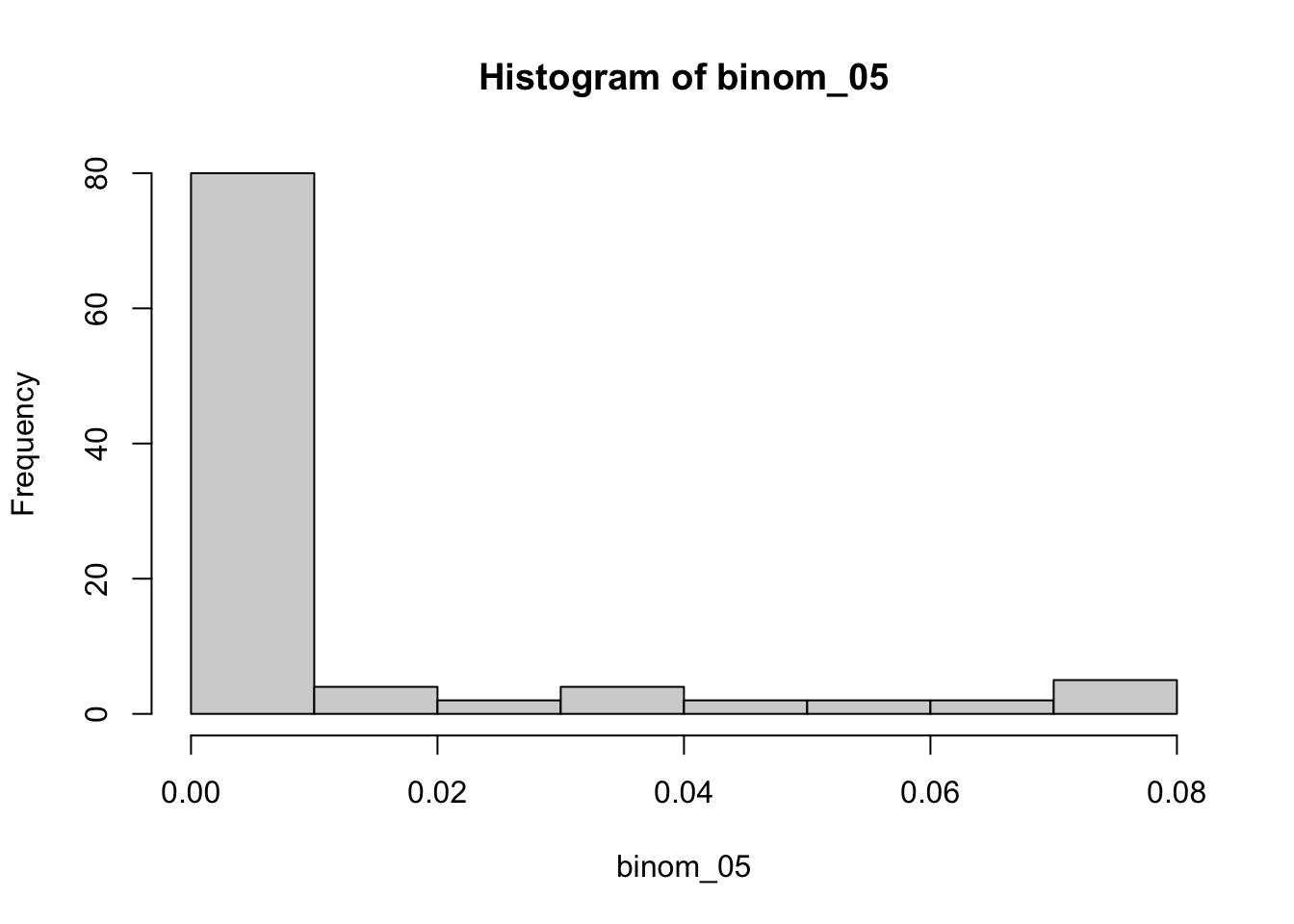
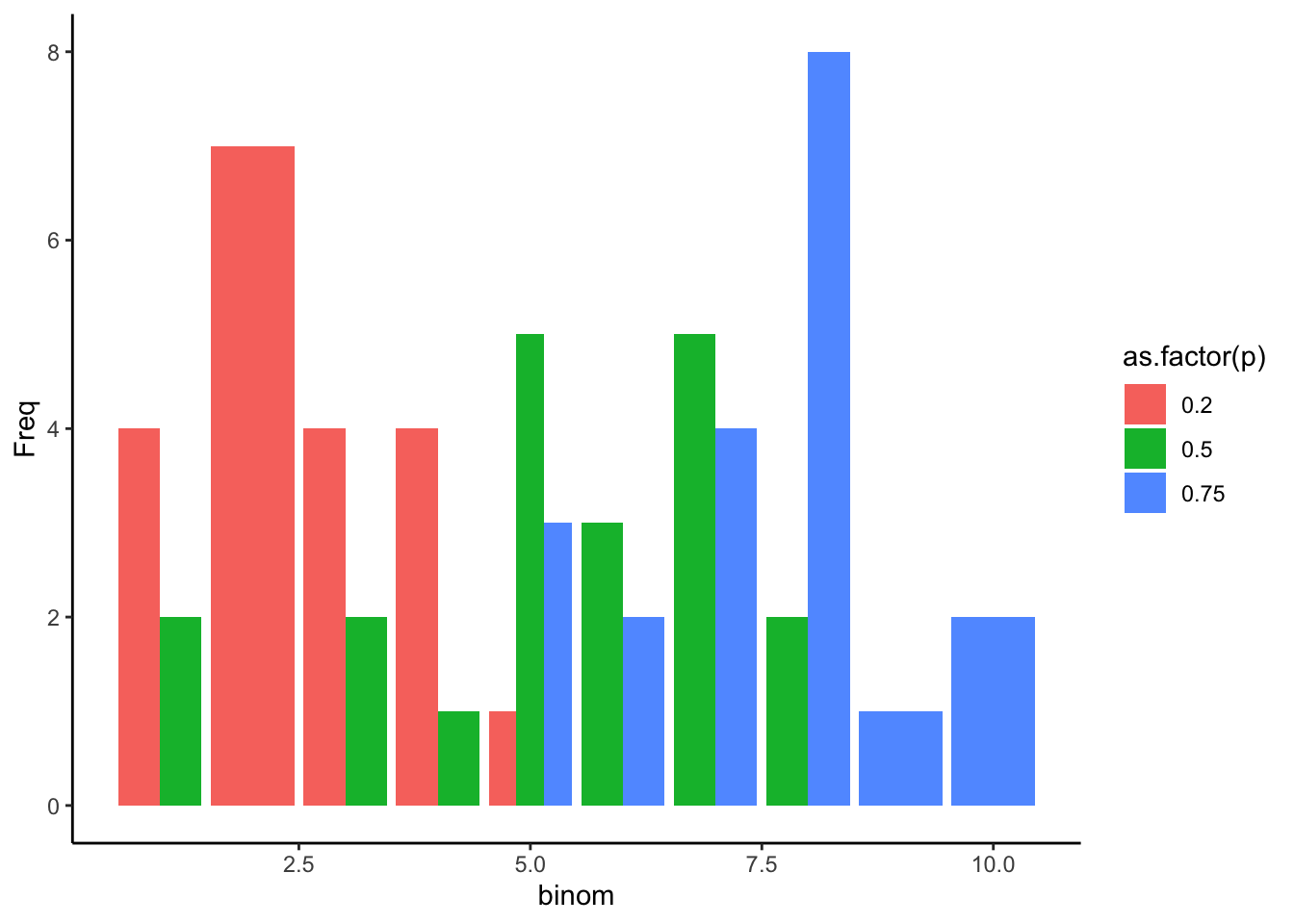
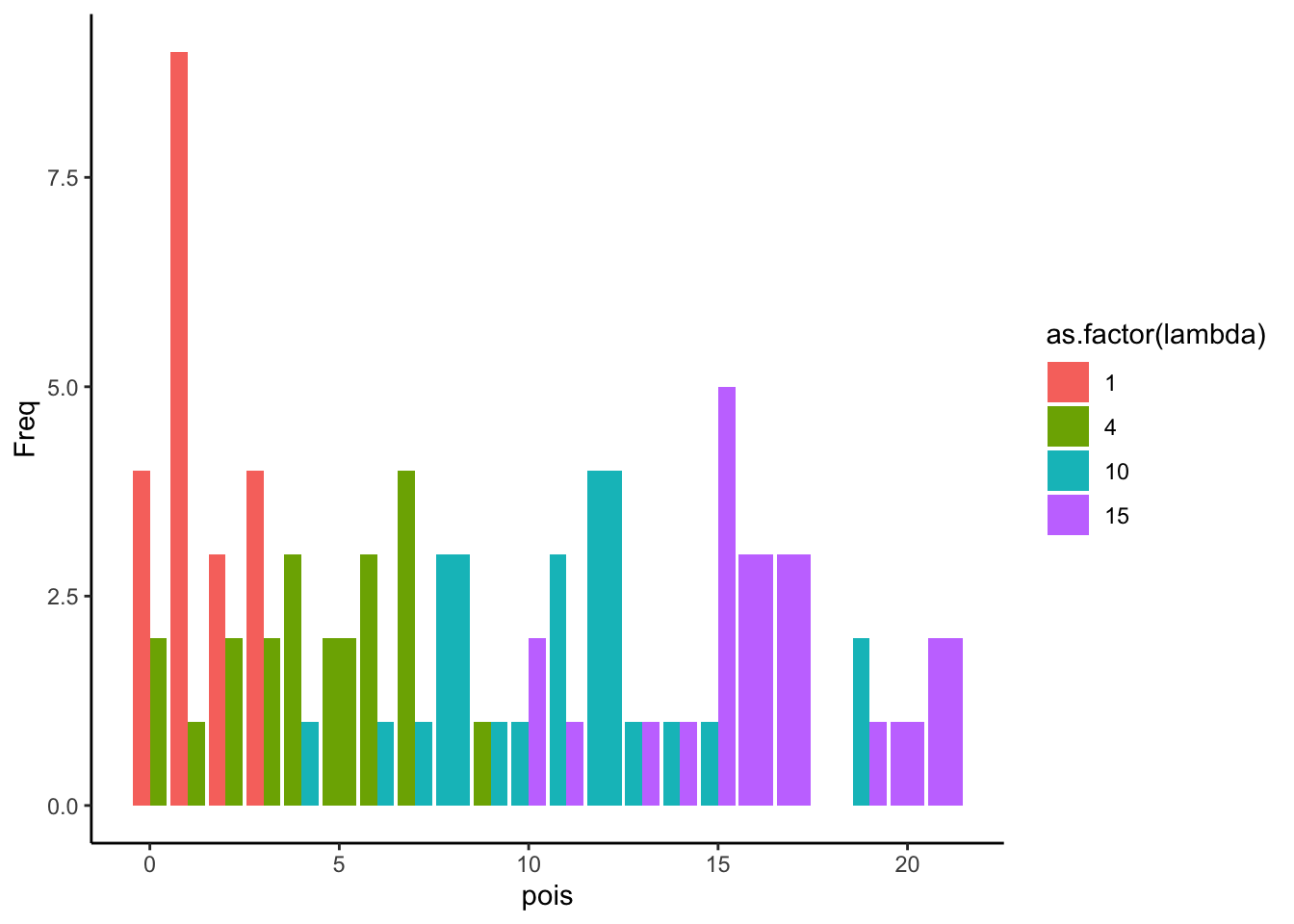
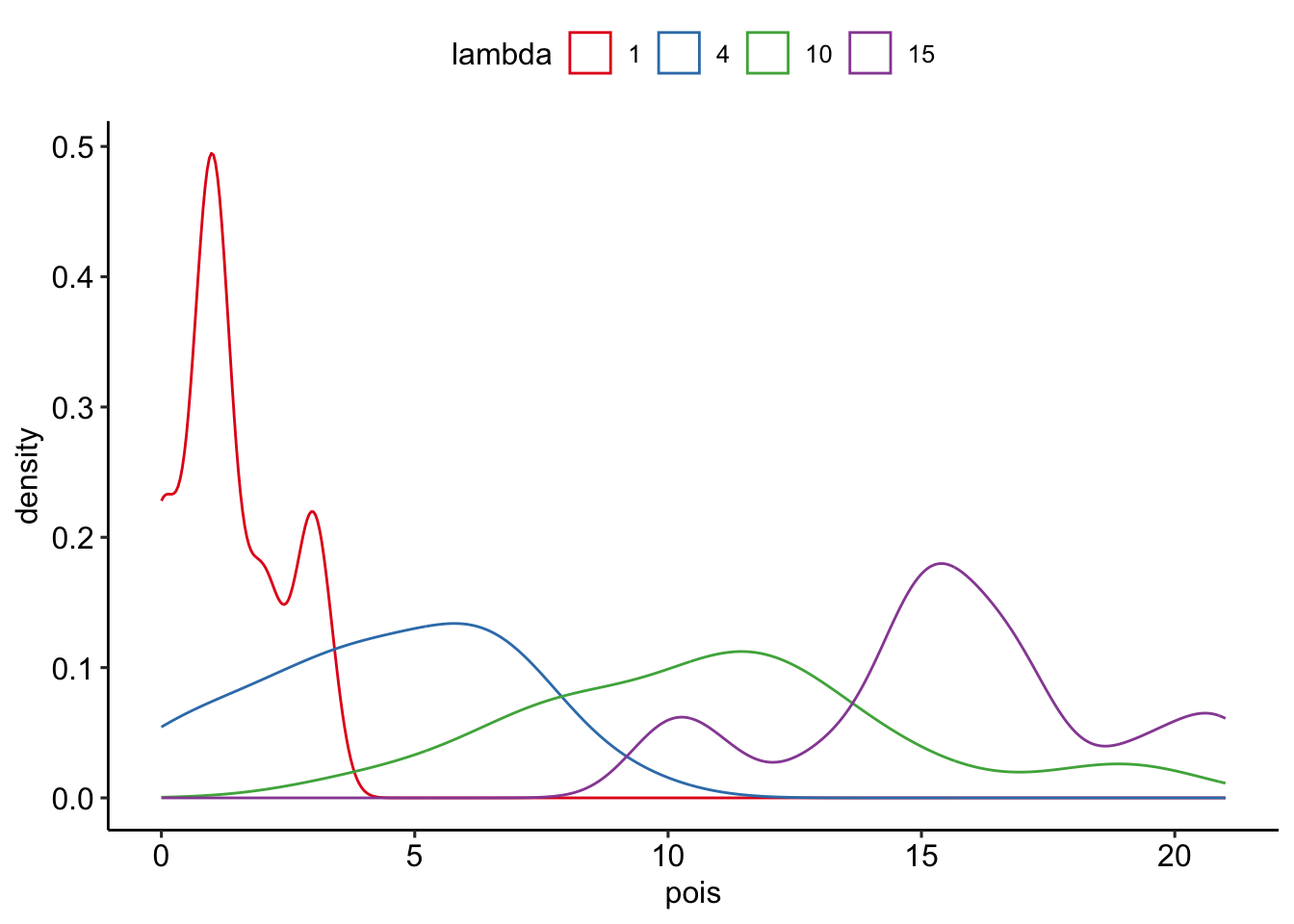
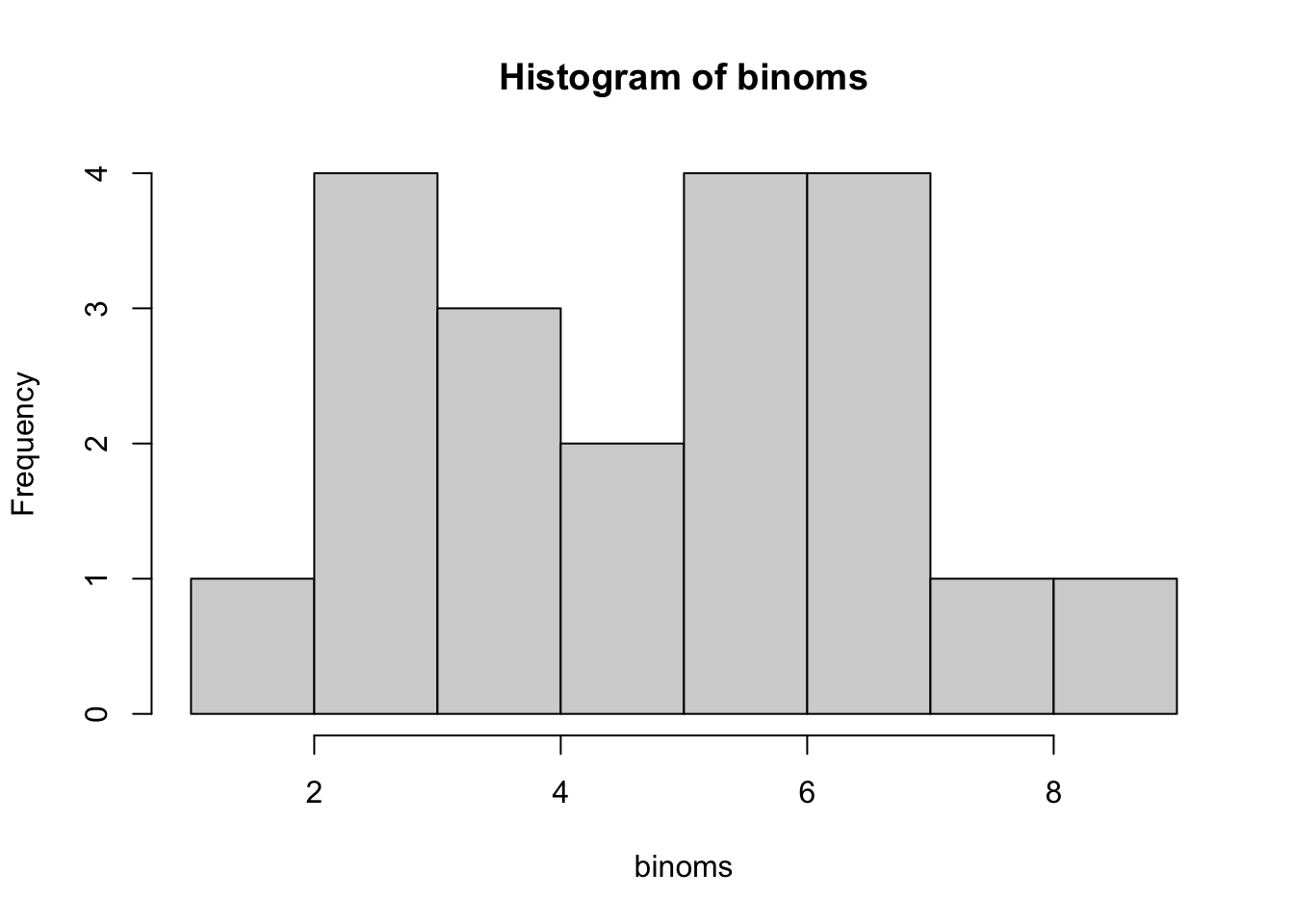
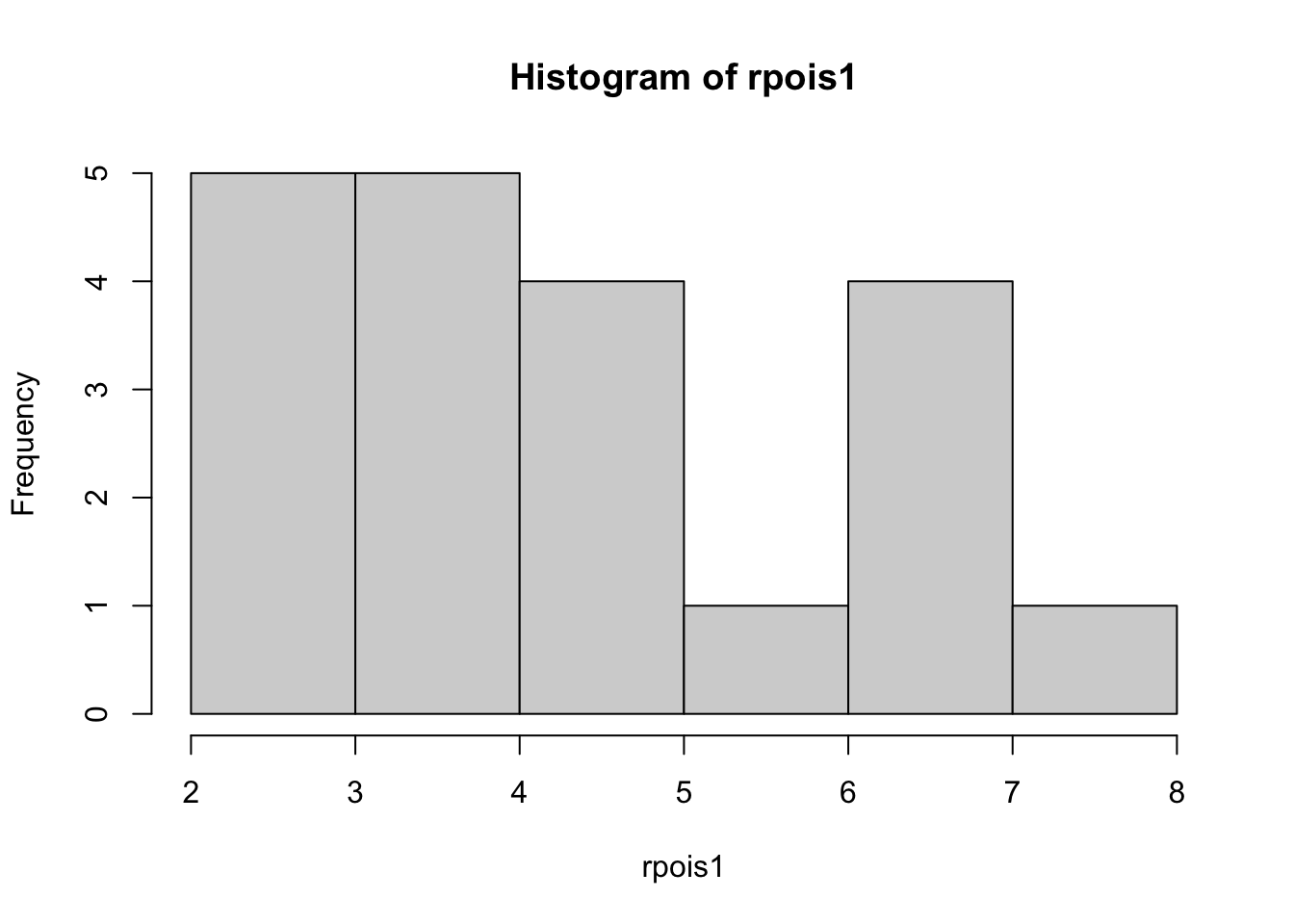
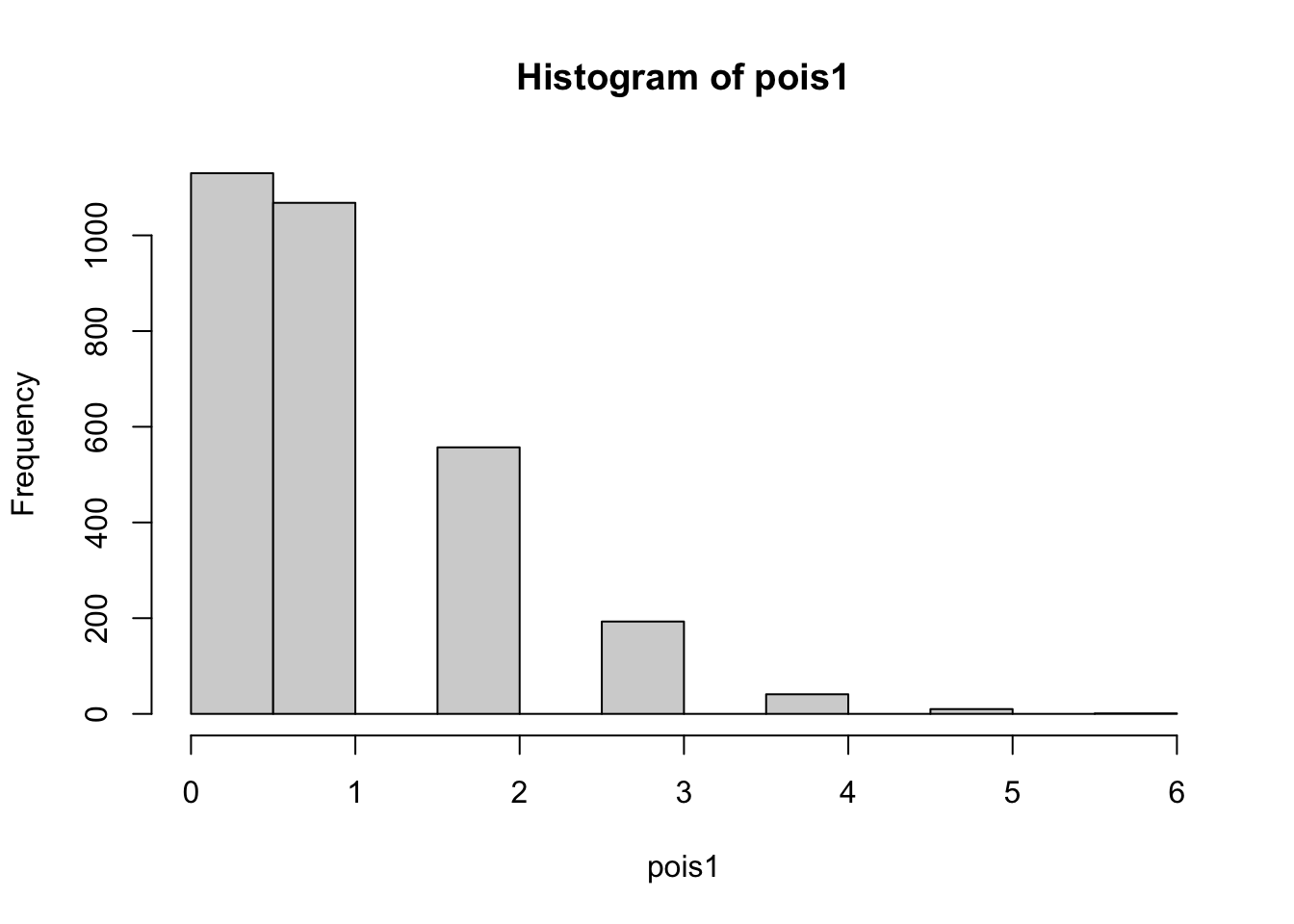
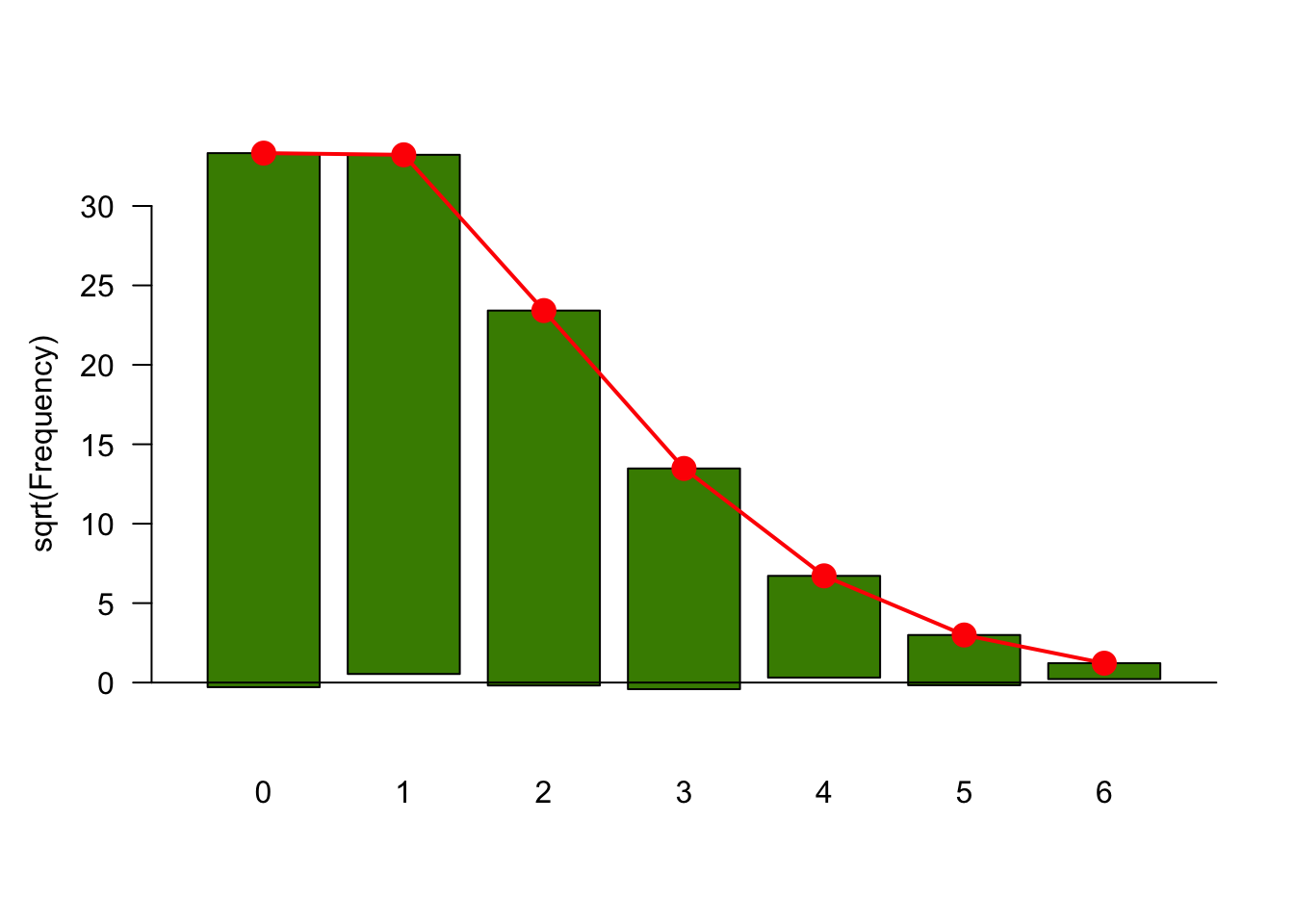
Fitting Distributions

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Bernoulli

?rbinom

# simulate 100 bernoulli trials
set.seed(42)
trials_025 <- rbinom(n = 100, size = 1, prob = 0.25)
trials_025

  [1] 1 1 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0
 [38] 0 1 0 0 0 0 1 0 1 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0
 [75] 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0

How does the distribution look like?

hist(trials_025)

Varying p (or \(\theta\))

set.seed(42)
ps <- c(0, 0.25, 0.5, 0.75)
data <- list()
for (p in ps) {
  trials <- rbinom(n = 100, size = 1, prob = p)
  df <- data.frame(successes = trials)
  df$p <- p
  data[[as.character(p)]] <- df
}
df_combined <- dplyr::bind_rows(data)
ggplot(df_combined, aes(x = successes, fill = as.factor(p))) +
  geom_histogram(position = "dodge", bins = 10) +
  ggpubr::theme_pubr()

Estimating \(\hat{theta}\)

We observe \(x_1, x_2, \dots, x_n\) outcomes from a Bernoulli trial and are interested in estimating the \(\theta\) parameter.

\[ \begin{align*} L(\theta) &= \prod_{i=1}^n \theta^{x_i}(1-\theta)^{(1-x_i)}\\ \ell(\theta) &= \log{\theta}\sum_{i=1}^n x_i + \log{(1-\theta)}\sum_{i=1}^n (1-x_i)\\ \end{align*} \]

In maximum likelihood estimation (MLE), our goal is to estimate the value of \(\theta\) such that the value of our likelihood function is maximized. More formally, in MLE we estimate \(\hat{\theta}\) such that

$$\[\begin{align*} \hat{\theta} &= \text{argmax} L(\theta) \end{align*}\]

\[\begin{align*} \dfrac{\partial\ell(\theta)}{\partial \theta} &= \dfrac{\sum_{i=1}^n x_i}{\theta} - \dfrac{\sum_{i=1}^n (1-x_i)}{1-\theta} \overset{\text{set}}{=}0\\ \sum_{i=1}^n x_i - \theta\sum_{i=1}^n x_i &= \theta\sum_{i=1}^n (1-x_i)\\ \hat{\theta}& = \dfrac{1}{n}\sum_{i=1}^n x_i\\ \dfrac{\partial^2 \ell(\theta)}{\partial \theta^2} &= \dfrac{-\sum_{i=1}^n x_i}{\theta^2} - \dfrac{\sum_{i=1}^n (1-x_i)}{(1-\theta)^2} < 0 \end{align*}\]$$

Calculating likelihood

trials_025[1:10]

 [1] 1 1 0 1 0 0 0 0 0 0

dbinom(x = trials_025, prob = 0.25, size = 1)[1:10]

 [1] 0.25 0.25 0.75 0.25 0.75 0.75 0.75 0.75 0.75 0.75

Calculating log-likelihood

log_likelihood_bernoulli <- function(p, data) {
  LL <- sum(dbinom(x = data, prob = p, size = 1, log = TRUE))
  return(LL)
}

log_likelihood_bernoulli(p = 0.5, data = trials_025)

[1] -69.31472

log_likelihood_bernoulli(p = 0.25, data = trials_025)

[1] -57.33213

log_likelihood_bernoulli(p = 0.1, data = trials_025)

[1] -67.66389

Where does the LL get maximum?

p <- seq(0, 1, 0.05)
ll <- sapply(p, log_likelihood_bernoulli, data = trials_025)
df <- data.frame(p = p, ll = ll)
ggplot(df, aes(p, ll)) +
  geom_point() + 
    theme_classic()

df %>% arrange(desc(ll))

      p         ll
1  0.25  -57.33213
2  0.30  -57.69724
3  0.20  -58.35801
4  0.35  -59.17331
5  0.15  -61.35152
6  0.40  -61.62466
7  0.45  -65.00114
8  0.10  -67.66389
9  0.50  -69.31472
10 0.55  -74.63333
11 0.60  -81.08698
12 0.05  -81.68474
13 0.65  -88.88719
14 0.70  -98.36754
15 0.75 -110.06552
16 0.80 -124.90014
17 0.85 -144.61237
18 0.90 -173.13067
19 0.95 -223.01781
20 0.00       -Inf
21 1.00       -Inf

Binomial

p <- 0.5
N <- 100
binom_05 <- dbinom(x = 0:100, prob = p, size = N)
sum(binom_05)

[1] 1

hist(binom_05)

N <- 10
p_vec <- c(0.2, 0.5, 0.75)

set.seed(42)
binoms.list <- list()
for (p in p_vec) {
  binoms <- rbinom(n = 20, prob = p, size = N)
  df <- data.frame(binom = binoms)
  df$p <- p
  binoms.list[[paste0(p)]] <- df
}
binoms.df <- bind_rows(binoms.list)
binoms.df.freq <- binoms.df %>%
  group_by(binom, p) %>%
  summarise(Freq = n())

`summarise()` has grouped output by 'binom'. You can override using the
`.groups` argument.

ggplot(binoms.df.freq, aes(binom, Freq, fill = as.factor(p))) +
  geom_bar(position = "dodge", stat = "identity") +
  theme_classic()

Poisson

lambdas <- c(1, 4, 10, 15)
set.seed(42)
pois.data <- list()
for (lambda in lambdas) {
  pois <- rpois(n = 20, lambda = lambda)
  df <- table(pois) %>% as.data.frame()
  df <- data.frame(pois = pois)

  df$lambda <- lambda
  pois.data[[paste0(lambda)]] <- df
}

pois.df <- bind_rows(pois.data)
pois.df.freq <- pois.df %>%
  group_by(pois, lambda) %>%
  summarise(Freq = n())

`summarise()` has grouped output by 'pois'. You can override using the
`.groups` argument.

ggplot(pois.df.freq, aes(pois, Freq, fill = as.factor(lambda))) +
  geom_bar(position = "dodge", stat = "identity") +
  theme_classic()

ggplot(pois.df, aes(pois, color = as.factor(lambda))) +
  geom_density() +
  ggpubr::theme_pubr() +
  scale_color_brewer(palette = "Set1", name = "lambda")

Why is a poisson used for rare events?

p <- 0.05
N <- 100
binoms <- rbinom(n = 20, prob = p, size = N)
 hist(binoms)

rpois1 <- rpois(n = 20, lambda = N*p )
hist(rpois1)

Investigating fit using vcd

We can use vcd to visualize if the data follows a poisson distribution.

library(vcd)

Loading required package: grid

pois1 <- rpois(n = 3000, lambda = 1)
hist(pois1)

The rootogram shows square root frequency on the y-axis and the observed ( in green bar or predicted - in red) quantity on the x-axis

pois1fit <- goodfit(x = pois1, type = "poisson")
rootogram(pois1fit, xlab = "", rect_gp = gpar(fill = "chartreuse4"))