Fast & memory efficient spearman correlation on sparse matrices

The previous post formulated a solution for calculating spearman correlation on sparse matrices. The trick was simple - we exploited the sparsity structure in our matrix to prevent it from being converted to a dense form at any step. For spearman correlation, following this line of thought is tricky, because the ranks are not sparse, at least not by default. We then used the property of covariance, where adding a constant quantity to all entries of a vector (or matrix) does not change its variance (or covariance) structure to come up with a solution that works great in theory and solves our purpose of keeping the memory footprint low. A notebook with an implementation here.

However, the time benchmarks look awful - though we ended up saving memory, SparseSpearmanCor() was atleast 2 times slower than the naive approach of densifying the matrix and calculating correlation using cor(as.matrix(X.sparse), method="spearman"). This in practise defeats the motivation - we are saving memory at the cost of speed.

Solution

The costliest step in my original implementation of SparseSpearmanCor() was a simple lookup operation: which(j == column) ,

where I fetch the non-zero entries in a column for calculating the rank, and this happens for all the columns (j stores the index of columns where there are non-zero entries).

I tried other ways of making this faster, such as by using fastmatch. But the actual speedup came from a simple thought - if we care about the non zero entries, I should just deal with them separately. So instead of doing repeated lookups, I just separate the non-zero entries out, do the rank sparsification operations on them and put them back into the sparse matrix. I call this implementation SparseSpearmanCor2() and you can find the implementation in the notebook, but here are some comparisons with the dense approach and the previous implementation SparseSpearmanCor().

The result is a function that calculates values 10x faster than any approach on large matrices (10000 x 5000):

Figure 1. Time benchmarks.

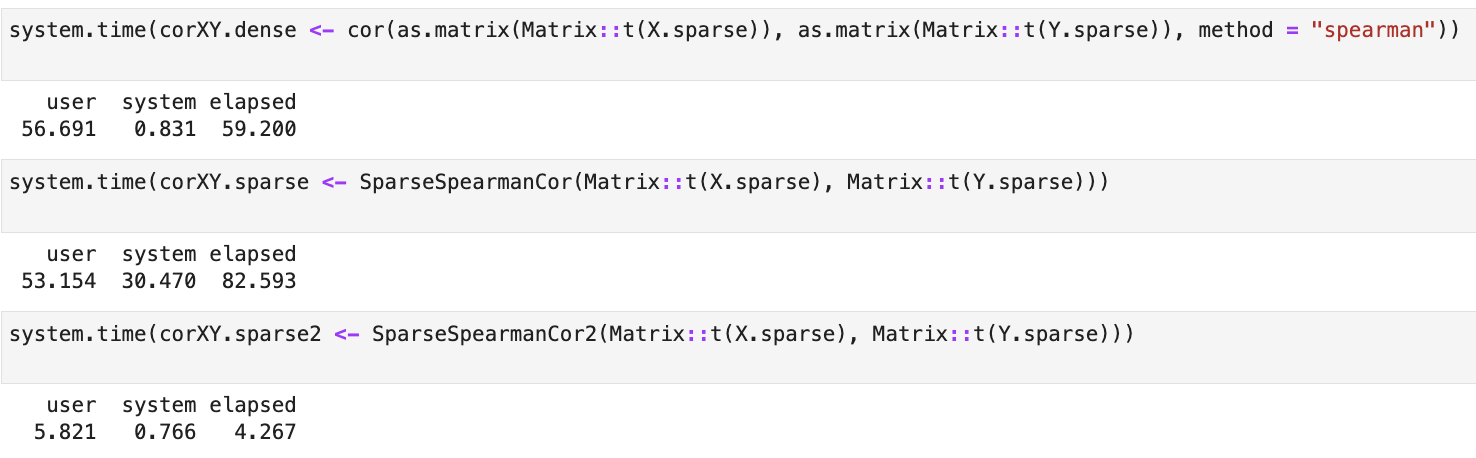
SparseSpearmanCor2() and time benchmarks are available in this notebook.