2. Chapter 2 - Linear Models: Least Squares Theory¶
import warnings
import pandas as pd
import proplot as plot
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from patsy import dmatrices
from scipy import stats
warnings.filterwarnings("ignore")
%pylab inline
plt.rcParams["axes.labelweight"] = "bold"
plt.rcParams["font.weight"] = "bold"
Populating the interactive namespace from numpy and matplotlib
scots_races_df = pd.read_csv("../data/ScotsRaces.tsv.gz", sep="\t")
scots_races_df.head()
| race | distance | climb | time | |
|---|---|---|---|---|
| 1 | GreenmantleNewYearDash | 2.5 | 0.65 | 16.08 |
| 2 | Carnethy5HillRace | 6.0 | 2.50 | 48.35 |
| 3 | CraigDunainHillRace | 6.0 | 0.90 | 33.65 |
| 4 | BenRhaHillRace | 7.5 | 0.80 | 45.60 |
| 5 | BenLomondHillRace | 8.0 | 3.07 | 62.27 |
A dataset contains a list of hill races in Scotland for the year. Explanatory variables:
distance of the race (in miles)
the cumulative climb (in thousands of feet)
print(scots_races_df[["time", "climb", "distance"]].mean(axis=0))
print(scots_races_df[["time", "climb", "distance"]].std(axis=0))
time 56.089714
climb 1.815314
distance 7.528571
dtype: float64
time 50.392617
climb 1.619151
distance 5.523936
dtype: float64
sns.pairplot(scots_races_df[["time", "climb", "distance"]])
<seaborn.axisgrid.PairGrid at 0x7f14f9889510>
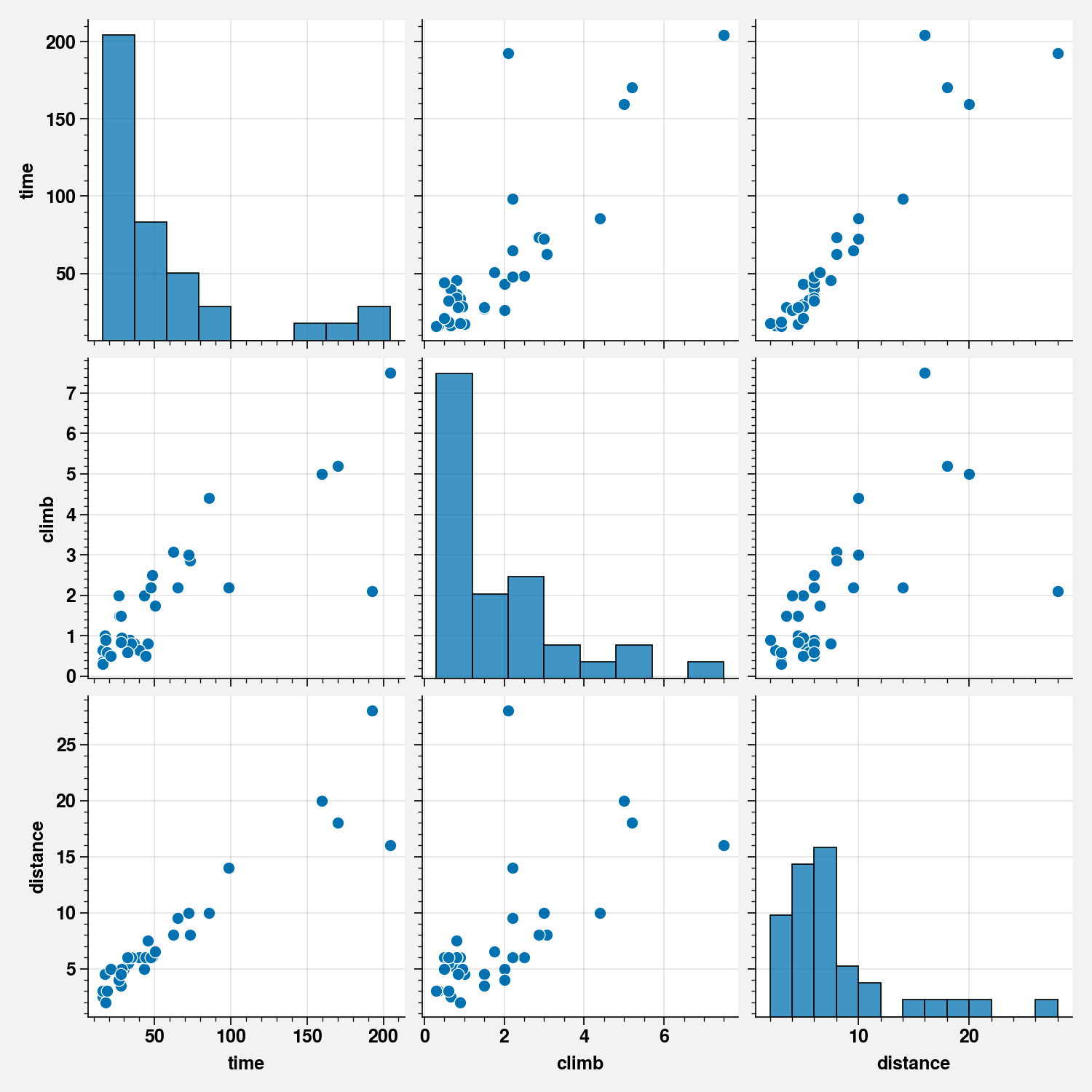
scots_races_df[["climb", "distance", "time"]].corr()
| climb | distance | time | |
|---|---|---|---|
| climb | 1.000000 | 0.652346 | 0.832654 |
| distance | 0.652346 | 1.000000 | 0.943094 |
| time | 0.832654 | 0.943094 | 1.000000 |
fit_cd = smf.ols(
formula="""time ~ climb + distance""",
data=scots_races_df[["climb", "distance", "time"]],
).fit()
print(fit_cd.summary())
OLS Regression Results
==============================================================================
Dep. Variable: time R-squared: 0.972
Model: OLS Adj. R-squared: 0.970
Method: Least Squares F-statistic: 549.9
Date: Tue, 12 Jan 2021 Prob (F-statistic): 1.67e-25
Time: 23:01:23 Log-Likelihood: -123.95
No. Observations: 35 AIC: 253.9
Df Residuals: 32 BIC: 258.6
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -13.1086 2.561 -5.119 0.000 -18.325 -7.892
climb 11.7801 1.221 9.651 0.000 9.294 14.266
distance 6.3510 0.358 17.751 0.000 5.622 7.080
==============================================================================
Omnibus: 7.207 Durbin-Watson: 1.983
Prob(Omnibus): 0.027 Jarque-Bera (JB): 6.967
Skew: 0.598 Prob(JB): 0.0307
Kurtosis: 4.829 Cond. No. 16.7
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Thus, adjusted for climb, the predicted record time increased by 6.34 minutes for every additional midle of distance
sns.distplot(fit_cd.resid, kde=False, color="slateblue")
<AxesSubplot:>
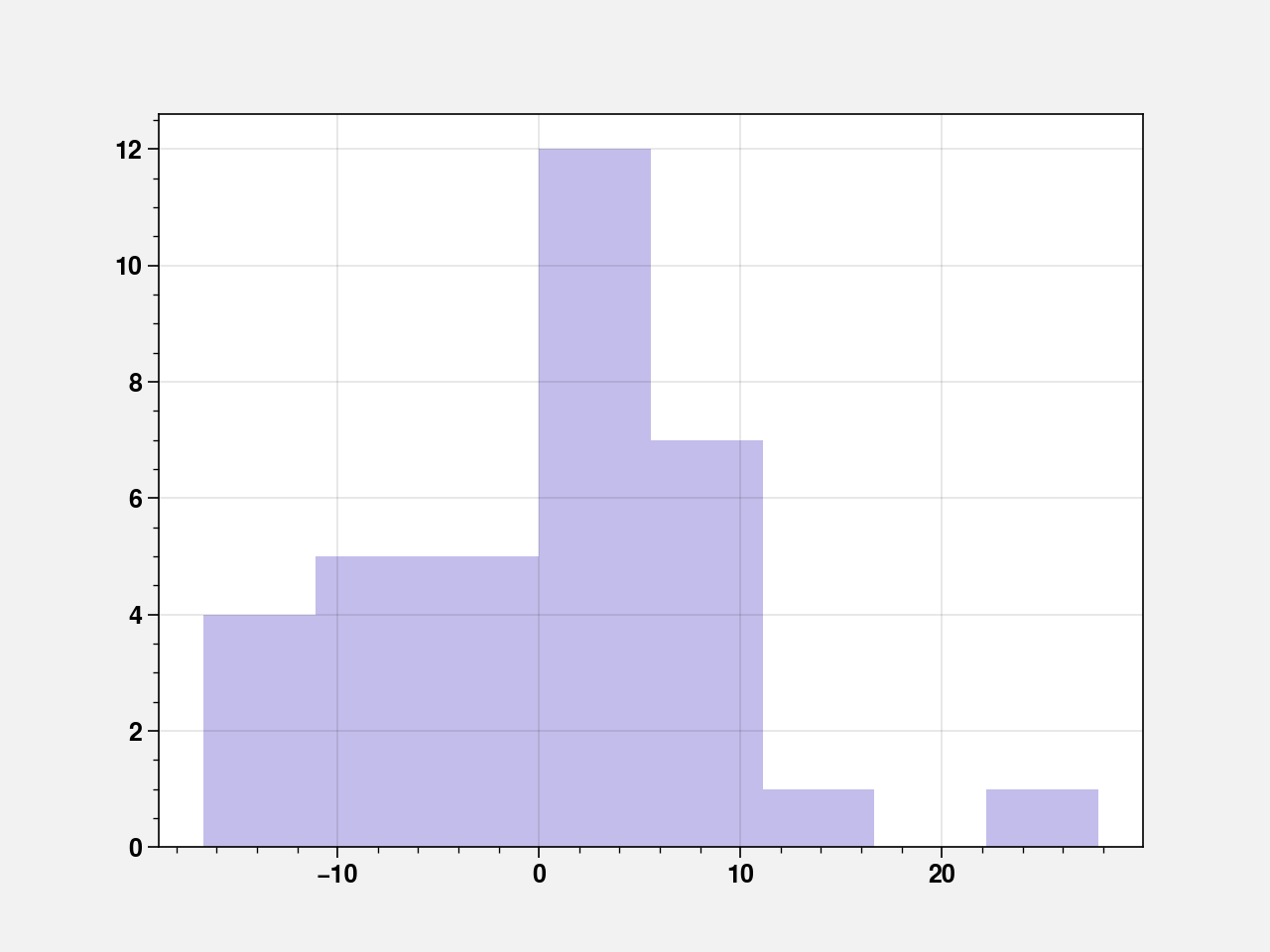
pd.Series(fit_cd.resid_pearson).quantile(q=[0, 0.25, 0.5, 0.75, 1])
0.00 -1.906667
0.25 -0.554349
0.50 0.127085
0.75 0.534341
1.00 3.178498
dtype: float64
print(stats.pearsonr(fit_cd.fittedvalues, fit_cd.resid))
(3.755818658506266e-15, 0.9999999999999806)
print(fit_cd.resid_pearson.mean(), fit_cd.resid_pearson.std())
6.483702463810914e-15 0.9561828874675148
fig, ax = plt.subplots(figsize=(5, 5))
ax.scatter(scots_races_df["distance"], fit_cd.resid_pearson)
<matplotlib.collections.PathCollection at 0x7f14f0e6b650>
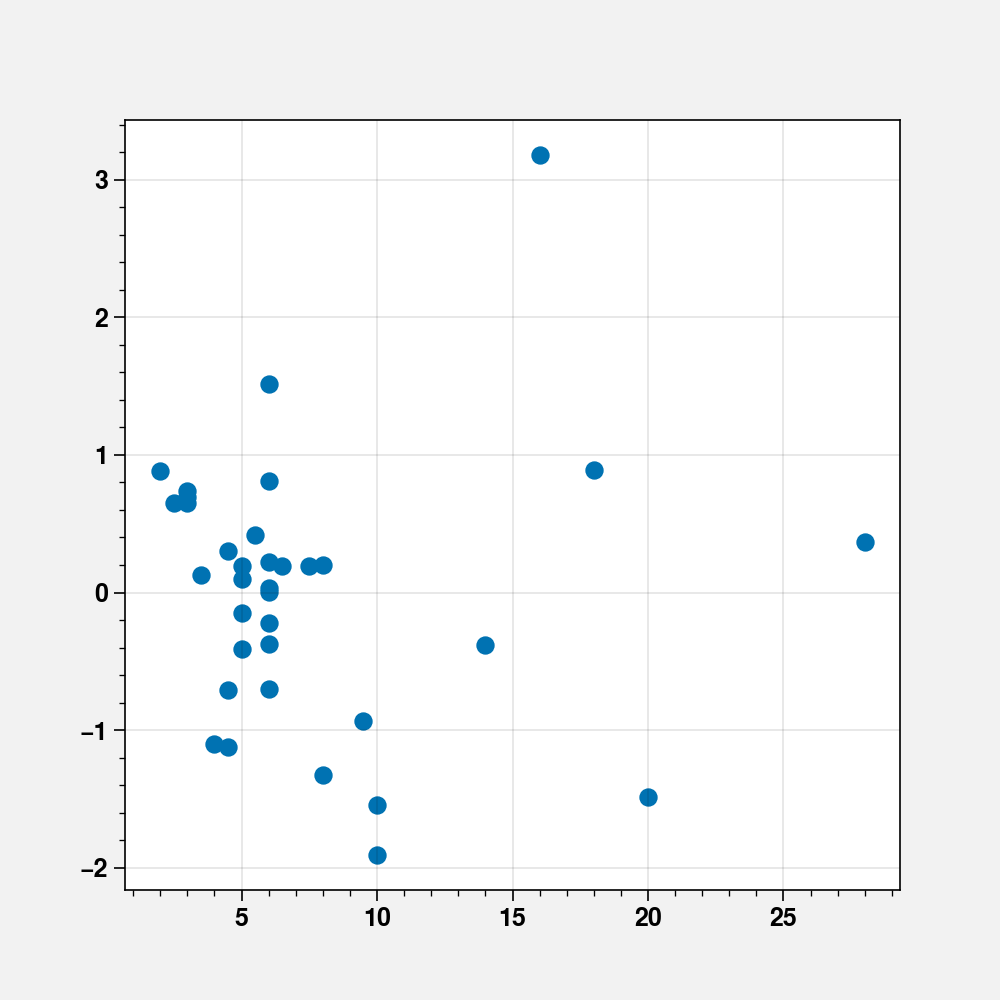
fig, ax = plt.subplots(figsize=(5, 5))
ax.scatter(fit_cd.fittedvalues, fit_cd.resid_pearson)
<matplotlib.collections.PathCollection at 0x7f14ee9f5710>
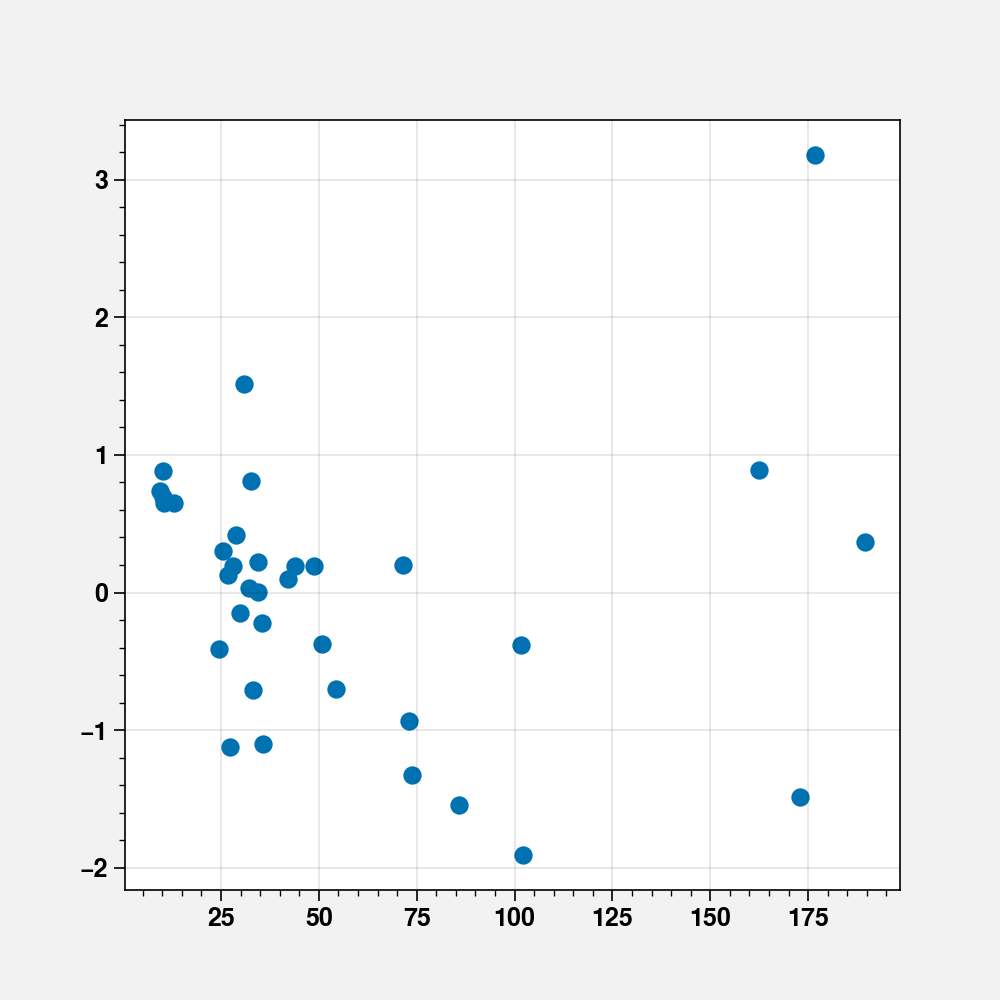
influence = fit_cd.get_influence()
summary_frame = influence.summary_frame()
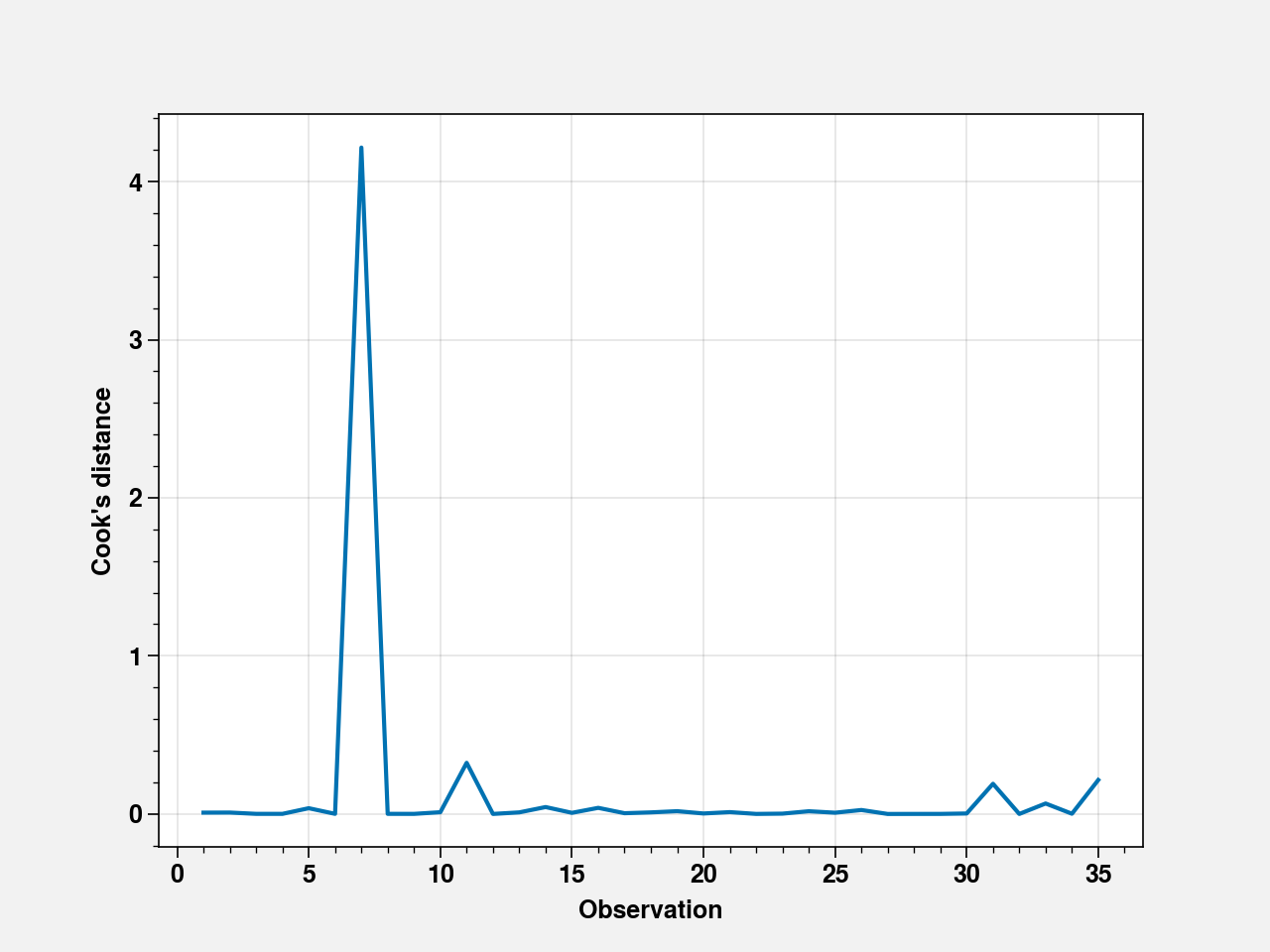
fig, ax = plt.subplots()
ax.plot(summary_frame["cooks_d"])
ax.set_xlabel("Observation")
ax.set_ylabel("Cook's distance")
Text(0, 0.5, "Cook's distance")
2.1. ANOVA¶
lm = smf.ols(
formula="""time ~ climb + distance""",
data=scots_races_df[["climb", "distance", "time"]],
).fit()
table = sm.stats.anova_lm(lm, typ=2)
print(table)
sum_sq df F PR(>F)
climb 7105.618848 1.0 93.139930 5.368815e-11
distance 24038.225642 1.0 315.091296 3.990140e-18
Residual 2441.270928 32.0 NaN NaN
# Change order
lm = smf.ols(
formula="""time ~ distance + climb""",
data=scots_races_df[["climb", "distance", "time"]],
).fit()
table = sm.stats.anova_lm(lm, typ=2)
print(table)
sum_sq df F PR(>F)
distance 24038.225642 1.0 315.091296 3.990140e-18
climb 7105.618848 1.0 93.139930 5.368815e-11
Residual 2441.270928 32.0 NaN NaN
lm = smf.ols(
formula="""time ~ climb + distance + climb:distance """,
data=scots_races_df[["climb", "distance", "time"]],
).fit()
table = sm.stats.anova_lm(lm, typ=2)
print(lm.summary())
OLS Regression Results
==============================================================================
Dep. Variable: time R-squared: 0.981
Model: OLS Adj. R-squared: 0.979
Method: Least Squares F-statistic: 524.1
Date: Tue, 12 Jan 2021 Prob (F-statistic): 1.24e-26
Time: 23:01:24 Log-Likelihood: -117.30
No. Observations: 35 AIC: 242.6
Df Residuals: 31 BIC: 248.8
Df Model: 3
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept -0.7672 3.906 -0.196 0.846 -8.733 7.199
climb 3.7133 2.365 1.570 0.126 -1.110 8.536
distance 4.9623 0.474 10.464 0.000 3.995 5.929
climb:distance 0.6598 0.174 3.786 0.001 0.304 1.015
==============================================================================
Omnibus: 9.175 Durbin-Watson: 1.509
Prob(Omnibus): 0.010 Jarque-Bera (JB): 14.024
Skew: -0.486 Prob(JB): 0.000901
Kurtosis: 5.945 Cond. No. 128.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.