4. Chapter 4 - Generalized Linear Models: Model Fitting and Inference¶
import warnings
import pandas as pd
import proplot as plot
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from patsy import dmatrices
from scipy import stats
warnings.filterwarnings("ignore")
%pylab inline
plt.rcParams["axes.labelweight"] = "bold"
plt.rcParams["font.weight"] = "bold"
Populating the interactive namespace from numpy and matplotlib
crabs_df = pd.read_csv("../data/Crabs.tsv.gz", sep="\t")
crabs_df.head()
| crab | y | weight | width | color | spine | |
|---|---|---|---|---|---|---|
| 1 | 1 | 8 | 3.05 | 28.3 | 2 | 3 |
| 2 | 2 | 0 | 1.55 | 22.5 | 3 | 3 |
| 3 | 3 | 9 | 2.30 | 26.0 | 1 | 1 |
| 4 | 4 | 0 | 2.10 | 24.8 | 3 | 3 |
| 5 | 5 | 4 | 2.60 | 26.0 | 3 | 3 |
formula = """y ~ width"""
response, predictors = dmatrices(formula, crabs_df, return_type="dataframe")
fit = sm.GLM(
response, predictors, family=sm.families.Poisson(link=sm.families.links.log())
).fit()
print(fit.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 173
Model: GLM Df Residuals: 171
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -461.59
Date: Tue, 12 Jan 2021 Deviance: 567.88
Time: 23:01:31 Pearson chi2: 544.
No. Iterations: 5
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -3.3048 0.542 -6.095 0.000 -4.368 -2.242
width 0.1640 0.020 8.216 0.000 0.125 0.203
==============================================================================
formula = """y ~ weight + width"""
response, predictors = dmatrices(formula, crabs_df, return_type="dataframe")
fit = sm.GLM(
response, predictors, family=sm.families.Poisson(link=sm.families.links.log())
).fit()
print(fit.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 173
Model: GLM Df Residuals: 170
Model Family: Poisson Df Model: 2
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -457.60
Date: Tue, 12 Jan 2021 Deviance: 559.90
Time: 23:01:31 Pearson chi2: 537.
No. Iterations: 5
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -1.2952 0.899 -1.441 0.150 -3.057 0.467
weight 0.4470 0.159 2.818 0.005 0.136 0.758
width 0.0461 0.047 0.986 0.324 -0.046 0.138
==============================================================================
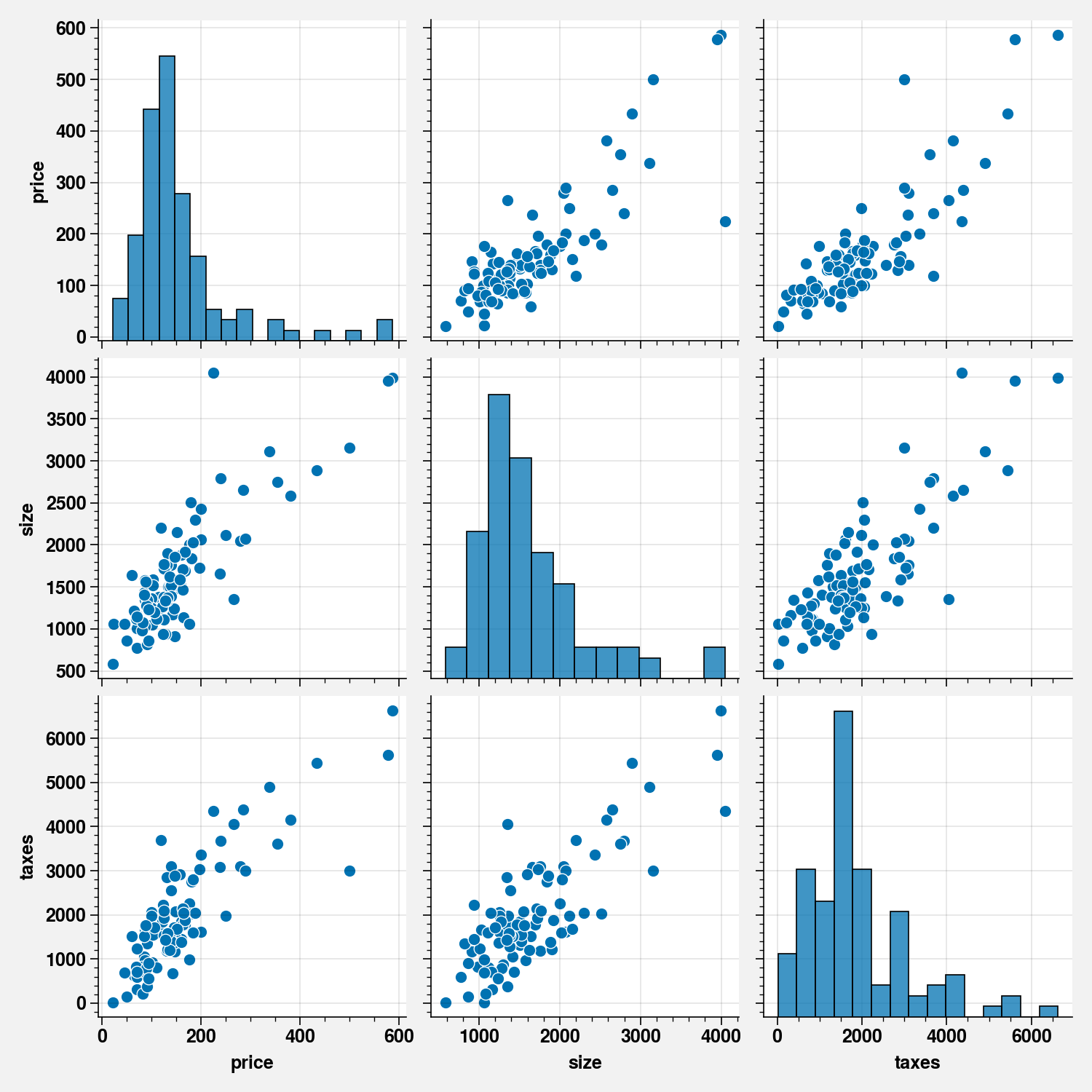
house_df = pd.read_csv("../data/Houses.tsv.gz", sep="\t")
sns.pairplot(house_df[["price", "size", "taxes"]])
<seaborn.axisgrid.PairGrid at 0x7f34688d0ed0>
from statsmodels.stats.anova import anova_lm
fit1 = smf.ols(formula="""price ~ size + new + baths + beds""", data=house_df).fit()
fit2 = smf.ols(
formula="""price ~ (size + new + baths + beds)**2""", data=house_df
).fit()
fit3 = smf.ols(
formula="""price ~ (size + new + baths + beds)**3""", data=house_df
).fit()
fit6 = smf.ols(
formula="""price ~ (size + new + baths + beds)**6""", data=house_df
).fit()
anova_results = anova_lm(fit1, fit2)
anova_results
| df_resid | ssr | df_diff | ss_diff | F | Pr(>F) | |
|---|---|---|---|---|---|---|
| 0 | 95.0 | 279624.077203 | 0.0 | NaN | NaN | NaN |
| 1 | 89.0 | 217916.368647 | 6.0 | 61707.708555 | 4.200377 | 0.000913 |
anova_results = anova_lm(fit2, fit1)
anova_results
| df_resid | ssr | df_diff | ss_diff | F | Pr(>F) | |
|---|---|---|---|---|---|---|
| 0 | 89.0 | 217916.368647 | 0.0 | NaN | NaN | NaN |
| 1 | 95.0 | 279624.077203 | -6.0 | -61707.708555 | 3.494115 | NaN |
anova_results
| df_resid | ssr | df_diff | ss_diff | F | Pr(>F) | |
|---|---|---|---|---|---|---|
| 0 | 89.0 | 217916.368647 | 0.0 | NaN | NaN | NaN |
| 1 | 95.0 | 279624.077203 | -6.0 | -61707.708555 | 3.494115 | NaN |
print(fit6.summary())
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.804
Model: OLS Adj. R-squared: 0.771
Method: Least Squares F-statistic: 24.85
Date: Tue, 12 Jan 2021 Prob (F-statistic): 3.27e-24
Time: 23:01:34 Log-Likelihood: -521.77
No. Observations: 100 AIC: 1074.
Df Residuals: 85 BIC: 1113.
Df Model: 14
Covariance Type: nonrobust
=======================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------------
Intercept -195.2928 159.474 -1.225 0.224 -512.369 121.783
size 0.2512 0.126 2.001 0.049 0.002 0.501
new 121.6101 119.714 1.016 0.313 -116.412 359.633
baths 151.0111 73.643 2.051 0.043 4.589 297.433
beds 39.8477 54.614 0.730 0.468 -68.740 148.435
size:new -1.8379 1.430 -1.285 0.202 -4.681 1.005
size:baths -0.1003 0.044 -2.268 0.026 -0.188 -0.012
size:beds -0.0370 0.035 -1.050 0.297 -0.107 0.033
new:baths 827.9218 717.935 1.153 0.252 -599.525 2255.368
new:beds -488.2639 407.026 -1.200 0.234 -1297.540 321.012
baths:beds -39.5669 24.330 -1.626 0.108 -87.942 8.809
size:new:baths 0.3423 0.241 1.423 0.158 -0.136 0.821
size:new:beds 0.7990 0.594 1.345 0.182 -0.382 1.980
size:baths:beds 0.0261 0.011 2.354 0.021 0.004 0.048
new:baths:beds -75.5298 76.579 -0.986 0.327 -227.788 76.729
size:new:baths:beds -0.1896 0.135 -1.402 0.164 -0.459 0.079
==============================================================================
Omnibus: 36.737 Durbin-Watson: 1.581
Prob(Omnibus): 0.000 Jarque-Bera (JB): 90.717
Skew: 1.339 Prob(JB): 2.00e-20
Kurtosis: 6.822 Cond. No. 1.21e+20
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 2.09e-30. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
4.1. Gamma GLMs for House Selling Price Data¶
formula = """price ~ size + new + beds + size:new + size:beds"""
response, predictors = dmatrices(formula, house_df, return_type="dataframe")
fit = sm.GLM(
response, predictors, family=sm.families.Gamma(link=sm.families.links.identity())
).fit()
print(fit.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: price No. Observations: 100
Model: GLM Df Residuals: 94
Model Family: Gamma Df Model: 5
Link Function: identity Scale: 0.10951
Method: IRLS Log-Likelihood: -517.66
Date: Tue, 12 Jan 2021 Deviance: 10.263
Time: 23:01:34 Pearson chi2: 10.3
No. Iterations: 21
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 44.3850 48.599 0.913 0.361 -50.867 139.637
size 0.0740 0.040 1.849 0.064 -0.004 0.152
new -60.0295 65.765 -0.913 0.361 -188.927 68.868
beds -22.7158 17.632 -1.288 0.198 -57.273 11.841
size:new 0.0538 0.038 1.432 0.152 -0.020 0.127
size:beds 0.0100 0.013 0.796 0.426 -0.015 0.035
==============================================================================
formula = """price ~ size + new + baths + beds"""
response, predictors = dmatrices(formula, house_df, return_type="dataframe")
fit_g1 = sm.GLM(
response, predictors, family=sm.families.Gamma(link=sm.families.links.identity())
).fit()
formula = """price ~ (size + new + baths + beds)**2"""
response, predictors = dmatrices(formula, house_df, return_type="dataframe")
fit_g2 = sm.GLM(
response, predictors, family=sm.families.Gamma(link=sm.families.links.identity())
).fit()
def anova_glm(model1, model2):
# Source: https://static1.squarespace.com/static/58332d815016e1b4077fe29f/t/5d3f1d90ed639e00011487c8/1564417425253/5.2_GLM+-+Comparing+Models-+F+Test+-+Errata.pdf
df_numerator = model2.df_model - model1.df_model
f_stat = (model1.deviance - model2.deviance) / (df_numerator * model2.scale)
df_denominator = model2.fittedvalues.shape[0] - model1.df_model
p_value = stats.f.sf(f_stat, df_numerator, df_denominator)
names = ["df_resid", "resid_deviance", "df_diff", "deviance", "F", "Pr(>F)"]
data = []
data.append((model1.df_resid, model1.deviance, " ", " ", " ", " "))
data.append(
(
model2.df_resid,
model2.deviance,
df_numerator,
model2.deviance,
f_stat,
p_value,
)
)
return pd.DataFrame(data, columns=names)
anova_results = anova_glm(fit_g1, fit_g2)
print(anova_results)
df_resid resid_deviance df_diff deviance F Pr(>F)
0 95 10.441719
1 89 9.872775 6 9.872775 0.843782 0.539286
4.2. TODO: Fix the anova_glm output¶
formula = """price ~ size + new + size:new"""
response, predictors = dmatrices(formula, house_df, return_type="dataframe")
fit = sm.GLM(
response, predictors, family=sm.families.Gamma(link=sm.families.links.identity())
).fit()
print(fit.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: price No. Observations: 100
Model: GLM Df Residuals: 96
Model Family: Gamma Df Model: 3
Link Function: identity Scale: 0.11020
Method: IRLS Log-Likelihood: -519.05
Date: Tue, 12 Jan 2021 Deviance: 10.563
Time: 23:01:34 Pearson chi2: 10.6
No. Iterations: 11
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -7.4509 12.974 -0.574 0.566 -32.880 17.978
size 0.0945 0.010 9.396 0.000 0.075 0.114
new -77.9046 64.582 -1.206 0.228 -204.483 48.674
size:new 0.0649 0.037 1.769 0.077 -0.007 0.137
==============================================================================
formula = """price ~ size + new + size:new"""
response, predictors = dmatrices(formula, house_df, return_type="dataframe")
fit = sm.GLM(
response, predictors, family=sm.families.Gaussian(link=sm.families.links.identity())
).fit()
print(fit.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: price No. Observations: 100
Model: GLM Df Residuals: 96
Model Family: Gaussian Df Model: 3
Link Function: identity Scale: 2703.8
Method: IRLS Log-Likelihood: -534.97
Date: Tue, 12 Jan 2021 Deviance: 2.5957e+05
Time: 23:01:34 Pearson chi2: 2.60e+05
No. Iterations: 3
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -22.2278 15.521 -1.432 0.152 -52.649 8.193
size 0.1044 0.009 11.082 0.000 0.086 0.123
new -78.5275 51.008 -1.540 0.124 -178.501 21.446
size:new 0.0619 0.022 2.855 0.004 0.019 0.104
==============================================================================
formula = """price ~ size + new + size:new"""
response, predictors = dmatrices(formula, house_df, return_type="dataframe")
fit = sm.GLM(
response, predictors, family=sm.families.Gaussian(link=sm.families.links.identity())
).fit()
print(fit.aic)
1077.9469818936211
formula = """price ~ size + new + beds + baths + size:new + size:beds + new:baths"""
response, predictors = dmatrices(formula, house_df, return_type="dataframe")
fit = sm.GLM(
response, predictors, family=sm.families.Gaussian(link=sm.families.links.identity())
).fit()
print(fit.aic)
1068.5650280217183