3. Chapter 3 - Normal Linear Models: Statistical Inference¶
import warnings
import pandas as pd
import proplot as plot
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from patsy import dmatrices
from scipy import stats
warnings.filterwarnings("ignore")
%pylab inline
plt.rcParams["axes.labelweight"] = "bold"
plt.rcParams["font.weight"] = "bold"
Populating the interactive namespace from numpy and matplotlib
stats.f.ppf(0.95, 2, 27) # 0.95 quantile of F dist. with df1=2, df2 =27
3.3541308285291986
1 - stats.f.pdf(3.364131, 2, 27) # right tail probability of non-central F
0.9602934531255635
house_df = pd.read_csv("../data/Houses.tsv.gz", sep="\t")
house_df
| case | taxes | beds | baths | new | price | size | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 3104 | 4 | 2 | 0 | 279.9 | 2048 |
| 1 | 2 | 1173 | 2 | 1 | 0 | 146.5 | 912 |
| 2 | 3 | 3076 | 4 | 2 | 0 | 237.7 | 1654 |
| 3 | 4 | 1608 | 3 | 2 | 0 | 200.0 | 2068 |
| 4 | 5 | 1454 | 3 | 3 | 0 | 159.9 | 1477 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 95 | 96 | 990 | 2 | 2 | 0 | 176.0 | 1060 |
| 96 | 97 | 3030 | 3 | 2 | 0 | 196.5 | 1730 |
| 97 | 98 | 1580 | 3 | 2 | 0 | 132.2 | 1370 |
| 98 | 99 | 1770 | 3 | 2 | 0 | 88.4 | 1560 |
| 99 | 100 | 1430 | 3 | 2 | 0 | 127.2 | 1340 |
100 rows × 7 columns
Data Description: Observations on recent homesales in Gainesville, Florida.
pd.concat([house_df.mean(), house_df.std()], axis=1).rename(
columns={0: "mean", 1: "sd"}
)
| mean | sd | |
|---|---|---|
| case | 50.500 | 29.011492 |
| taxes | 1908.390 | 1235.825663 |
| beds | 3.000 | 0.651339 |
| baths | 1.960 | 0.567112 |
| new | 0.110 | 0.314466 |
| price | 155.331 | 101.262213 |
| size | 1629.280 | 666.941702 |
fit = smf.ols(formula="""price ~ size + new""", data=house_df).fit()
print(fit.summary())
model_residuals = fit.resid
sd_model_residuals = model_residuals.std()
print("Residual SE: {}".format(np.round(sd_model_residuals, 2)))
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.723
Model: OLS Adj. R-squared: 0.717
Method: Least Squares F-statistic: 126.3
Date: Tue, 12 Jan 2021 Prob (F-statistic): 9.79e-28
Time: 23:01:27 Log-Likelihood: -539.05
No. Observations: 100 AIC: 1084.
Df Residuals: 97 BIC: 1092.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -40.2309 14.696 -2.738 0.007 -69.399 -11.063
size 0.1161 0.009 13.204 0.000 0.099 0.134
new 57.7363 18.653 3.095 0.003 20.715 94.757
==============================================================================
Omnibus: 12.906 Durbin-Watson: 1.483
Prob(Omnibus): 0.002 Jarque-Bera (JB): 29.895
Skew: 0.370 Prob(JB): 3.22e-07
Kurtosis: 5.574 Cond. No. 6.32e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.32e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Residual SE: 53.33
Interpretation:
- $H_0: \beta_1 = \beta_2 = 0$ The F-statistic with df1 = 2, df2 = 100-3 = 97 is 126.3 with a low p-value which is not surprising since the null is too strict. In some sense the probability of both the coefficients of size and new being 0 is low.
- Coeff of new: Having "adjusted" for size the coefficient of new is still significant
95%CI for the mean selling price of new homes at the mean size of the new homes, 2354.73 square feet:
prediction = fit.get_prediction({"size": 2354.73, "new": 1})
prediction.summary_frame()
| mean | mean_se | mean_ci_lower | mean_ci_upper | obs_ci_lower | obs_ci_upper | |
|---|---|---|---|---|---|---|
| 0 | 290.963953 | 16.245718 | 258.720701 | 323.207205 | 179.270051 | 402.657856 |
Interpretation: If the model truly holds, the ‘mean_ci_lower’ and ‘mean_ci_upper’ reflects the 95% confidence interval where the population mean will lie. While ‘obs_ci_lower’ and ‘obs_ci_upper’ reflects the 95% CI where the future (predicted) will lie.
3.1. TODO: Derivation of the CI for mean and future y¶
Also see CrossValidated
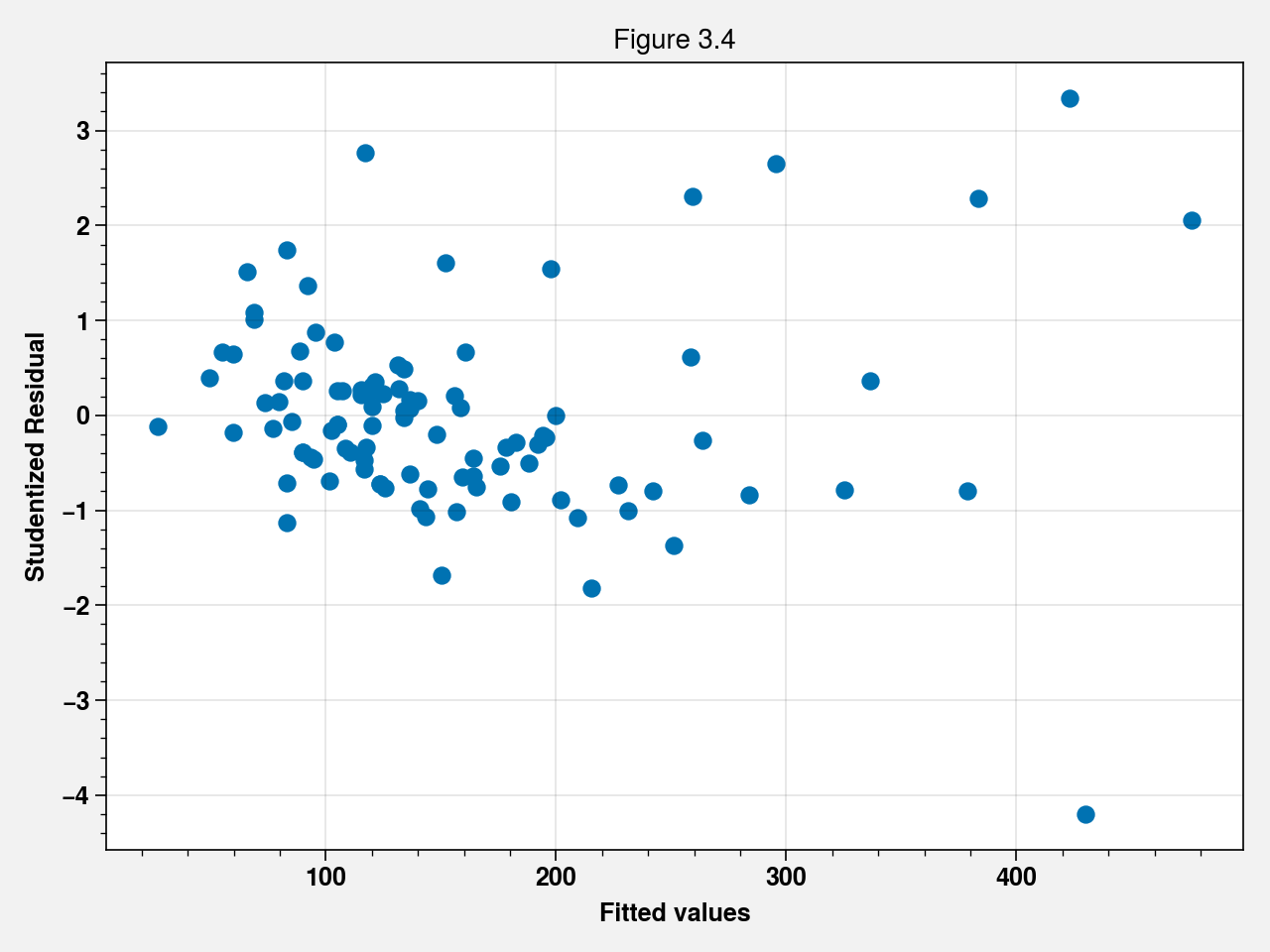
fig, ax = plt.subplots()
ax.scatter(fit.fittedvalues, fit.get_influence().resid_studentized_internal)
ax.set_xlabel("Fitted values")
ax.set_ylabel("Studentized Residual")
ax.set_title("Figure 3.4")
fig.tight_layout()
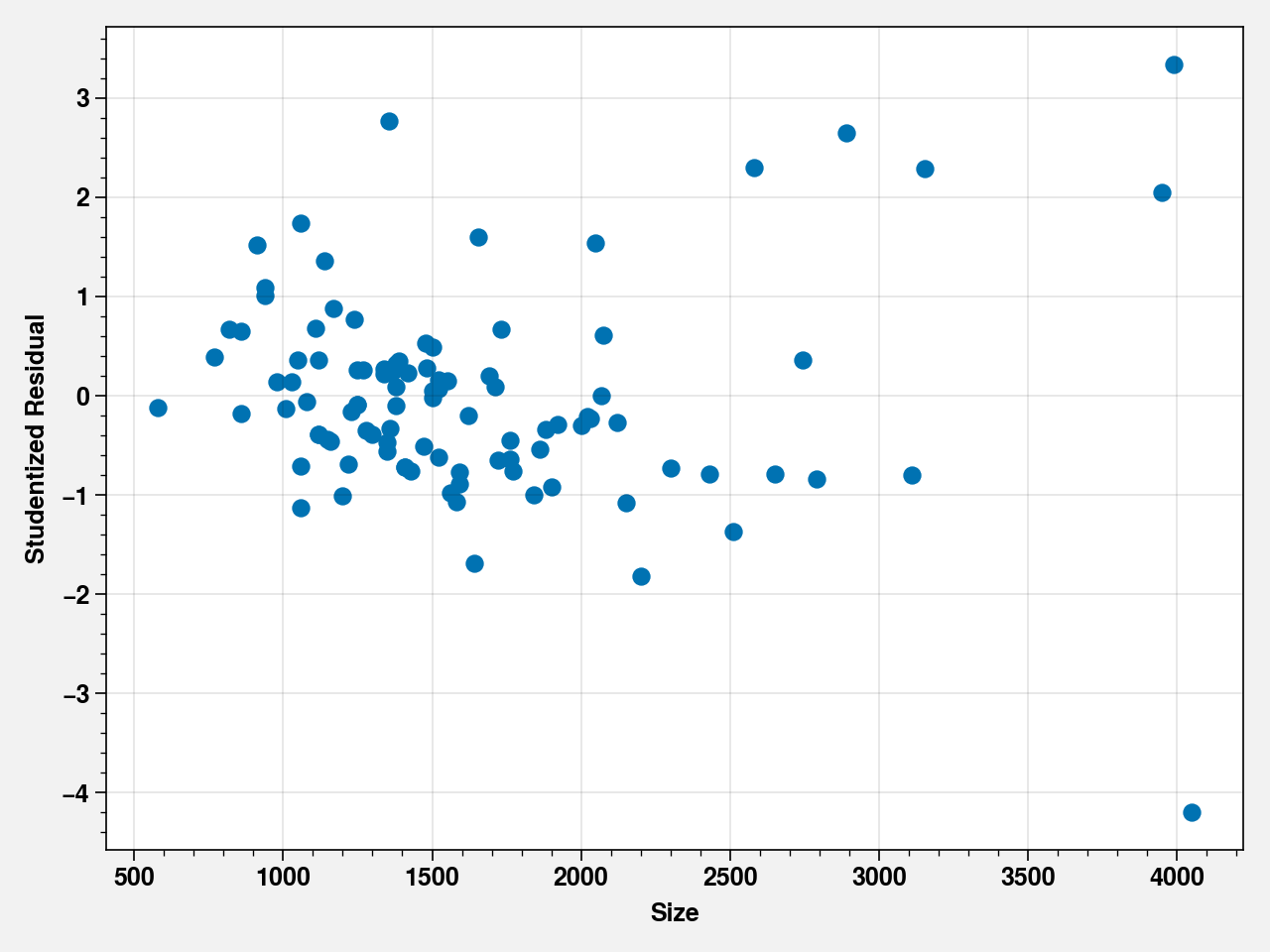
fig, ax = plt.subplots()
ax.scatter(house_df["size"], fit.get_influence().resid_studentized_internal)
ax.set_xlabel("Size")
ax.set_ylabel("Studentized Residual")
fig.tight_layout()
cooks_distance = fit.get_influence().cooks_distance[0]
plt.plot(cooks_distance)
[<matplotlib.lines.Line2D at 0x7fe63ac0eb50>]
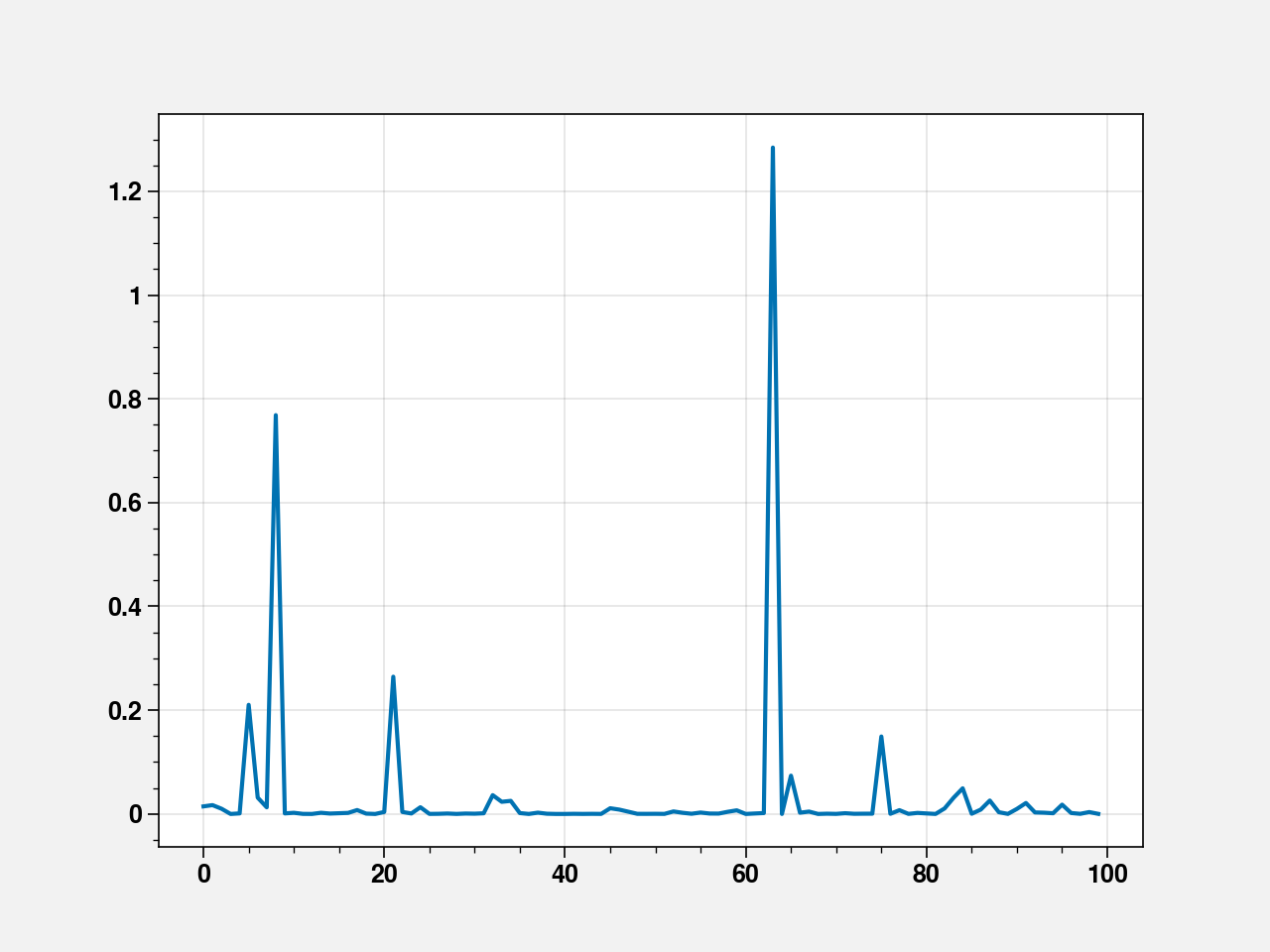
Observation 64 seems influential. Let’s remove it and refit.
fit = smf.ols(
formula="""price ~ size + new""", data=house_df.loc[cooks_distance < 1]
).fit()
print(fit.summary())
model_residuals = fit.resid
sd_model_residuals = model_residuals.std()
print("Residual SE: {}".format(np.round(sd_model_residuals, 2)))
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.772
Model: OLS Adj. R-squared: 0.767
Method: Least Squares F-statistic: 162.5
Date: Tue, 12 Jan 2021 Prob (F-statistic): 1.52e-31
Time: 23:01:28 Log-Likelihood: -524.21
No. Observations: 99 AIC: 1054.
Df Residuals: 96 BIC: 1062.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -63.1545 14.252 -4.431 0.000 -91.444 -34.865
size 0.1328 0.009 15.138 0.000 0.115 0.150
new 41.3062 17.327 2.384 0.019 6.913 75.700
==============================================================================
Omnibus: 8.263 Durbin-Watson: 1.480
Prob(Omnibus): 0.016 Jarque-Bera (JB): 7.876
Skew: 0.640 Prob(JB): 0.0195
Kurtosis: 3.520 Cond. No. 6.42e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.42e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Residual SE: 48.48
\(R^2\) sees a considerable improvement. Next we check for an interaction:
fit = smf.ols(formula="""price ~ size + new + size:new""", data=house_df.loc[cooks_distance<1]).fit()
print(fit.summary())
model_residuals = fit.resid
sd_model_residuals = model_residuals.std()
print("Residual SE: {}".format(np.round(sd_model_residuals, 2)))
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.782
Model: OLS Adj. R-squared: 0.775
Method: Least Squares F-statistic: 113.7
Date: Tue, 12 Jan 2021 Prob (F-statistic): 2.52e-31
Time: 23:01:28 Log-Likelihood: -521.95
No. Observations: 99 AIC: 1052.
Df Residuals: 95 BIC: 1062.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -48.2431 15.686 -3.075 0.003 -79.385 -17.102
size 0.1230 0.010 12.536 0.000 0.104 0.142
new -52.5122 47.630 -1.102 0.273 -147.070 42.046
size:new 0.0434 0.021 2.109 0.038 0.003 0.084
==============================================================================
Omnibus: 14.139 Durbin-Watson: 1.508
Prob(Omnibus): 0.001 Jarque-Bera (JB): 16.134
Skew: 0.807 Prob(JB): 0.000314
Kurtosis: 4.144 Cond. No. 1.76e+04
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.76e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
Residual SE: 47.39
The increase in \(R^2\) is minimal.
3.2. Simpson’s paradox¶
Consider adding beds as another explanatory variable.
stats.pearsonr(house_df['beds'], house_df['price'])
(0.39395702205835825, 5.006768706208423e-05)
Thus, beds is modestly correlated with price. Let’s include it in the model and see how the fit changes.
fit = smf.ols(formula="""price ~ size + new""", data=house_df).fit()
print(fit.summary())
model_residuals = fit.resid
sd_model_residuals = model_residuals.std()
print("Residual SE: {}".format(np.round(sd_model_residuals, 2)))
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.723
Model: OLS Adj. R-squared: 0.717
Method: Least Squares F-statistic: 126.3
Date: Tue, 12 Jan 2021 Prob (F-statistic): 9.79e-28
Time: 23:01:28 Log-Likelihood: -539.05
No. Observations: 100 AIC: 1084.
Df Residuals: 97 BIC: 1092.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -40.2309 14.696 -2.738 0.007 -69.399 -11.063
size 0.1161 0.009 13.204 0.000 0.099 0.134
new 57.7363 18.653 3.095 0.003 20.715 94.757
==============================================================================
Omnibus: 12.906 Durbin-Watson: 1.483
Prob(Omnibus): 0.002 Jarque-Bera (JB): 29.895
Skew: 0.370 Prob(JB): 3.22e-07
Kurtosis: 5.574 Cond. No. 6.32e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.32e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Residual SE: 53.33
fit = smf.ols(formula="""price ~ size + new + beds""", data=house_df).fit()
print(fit.summary())
model_residuals = fit.resid
sd_model_residuals = model_residuals.std()
print("Residual SE: {}".format(np.round(sd_model_residuals, 2)))
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.724
Model: OLS Adj. R-squared: 0.715
Method: Least Squares F-statistic: 83.97
Date: Tue, 12 Jan 2021 Prob (F-statistic): 9.68e-27
Time: 23:01:28 Log-Likelihood: -538.78
No. Observations: 100 AIC: 1086.
Df Residuals: 96 BIC: 1096.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -25.1998 25.602 -0.984 0.327 -76.020 25.620
size 0.1205 0.011 11.229 0.000 0.099 0.142
new 54.8996 19.113 2.872 0.005 16.961 92.838
beds -7.2927 10.159 -0.718 0.475 -27.458 12.872
==============================================================================
Omnibus: 13.929 Durbin-Watson: 1.496
Prob(Omnibus): 0.001 Jarque-Bera (JB): 41.568
Skew: 0.277 Prob(JB): 9.41e-10
Kurtosis: 6.110 Cond. No. 8.80e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.8e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Residual SE: 53.19
Including beds leads to a reduced \(R^2\)!! Thus, once size and new are in the model, it does not help to add beds. Although the marginal effect of beds is positive (as shown by the modest positive correlation), the estimated partial effect of beds is negative. This illustrates Simpson’s paradox.
3.3. Partial Correlation¶
regress_sizenew_on_price = smf.ols(formula="""price ~ size + new""", data=house_df).fit()
regress_sizenew_on_bed = smf.ols(formula="""beds ~ size + new""", data=house_df).fit()
stats.pearsonr(regress_sizenew_on_price.resid, regress_sizenew_on_bed.resid)
(-0.07307200731424245, 0.4699872574144025)
Partial correlation between selling price and beds. Found using 1) finding the residuals for predicting selling price using size and new 2) finding the residual for predicting beds using size and new and 3) correlating the residuals in 1 and 2.
3.4. TODO: Testing contrats as a general linear hypothesis¶
from statsmodels.stats.libqsturng import psturng, qsturng
qsturng(0.95, 10, 190)
4.52786052558441
stats.t.ppf(1-0.05/(2*45), 190)
3.3113791139604563